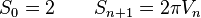| Цитата |
|---|
| Павел Чижов пишет: Что меня удивляло в этих формулах, это то, что площадь квадрата к площади куба (вполне естественно) относится как 1\6, а площадь круга к площади сферы как 1\4 |
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности.