| Цитата |
|---|
BETEP IIEPEMEH 04.02.2010 в 20:03:25
Соответственно, это тоже неверно, поскольку потенциал U не имеет постоянного знака на интервале (0, +inf).
Валерий Пивоваров 05.02.2010 09:34:09
Мы здесь ведем речь о ПОТЕНЦИАЛЕ, то есть, рассматриваем ОДНУ ТОЧКУ потенциального поля (или эквипотенциальную поверхность, но об этом нам еще рано говорить).
Вы же говорите о РАЗНОСТИ ПОТЕНЦИАЛОВ, вытекающей из рассмотрения интервала, состоящего из ДВУХ ТОЧЕК поля. Как бы близко или далеко не находились они друг от друга, но это две разные точки поля.
BETEP IIEPEMEH 05.02.2010 в 11:19:01
Ну а это уже откровенное вранье. |
Ну, конечно, «вранье», ибо, что еще может сказать несогласный с Вашей «точкой зрения» оппонент. Помнится, Вы 27.01.2010 18:18:01 меня пожурили за выражение «разошелся» и я с Вами согласился, ибо надо быть скромнее всем, в том числе и мне. Но Вам, выходит, можно…
Кстати, Вы видели интервал между одной точкой? Я, нет.
И еще. Как тогда понимать Ваши слова от 01.02.2010 в 11:01:03?
| Цитата |
|---|
BETEP IIEPEMEH 01.02.2010 в 11:01:03
Напоминаю, что потенциальная энергия - это работа, которую необходимо совершить, чтобы перенести тело из одной точки в другую (в поле консервативных сил). И, в зависимости от того, какие мы точки выбираем для определения потенциальной энергии, она у нас оказывается положительной или отрицательной. То же самое касается и потенциала. |
Здесь Вы конкретно говорите о разности энергий и, соответственно, о разности потенциалов. Теперь, Вы против?
| Цитата |
|---|
BETEP IIEPEMEH 05.02.2010 в 11:19:01
…сделайте и приведите свой собственный вывод выражения для потенциала, вместо того чтобы бездумно списывать его из энциклопедии. Не можете или не хотите - тема про отрицательность потенциальной энергии закрыта. |
Могу, и странно, что Вы в этом сомневаетесь. Однако мой вывод дает точно такой же результат, как и в Энциклопедии. Не понятно другое, чем Вам не нравится приведенный в Энциклопедии результат?
| Цитата |
|---|
BETEP IIEPEMEH 05.02.2010 в 11:19:01
В самом деле, перепишем выражение для орбитальной скорости в более общем правильном виде:
mV^2/R = m grad U
Здесь величины взяты по модулю. |
Хороший пример. Если обе части этого уравнения поделить на массу (m), то в левой части получим напряженность гравитационного поля (g), ибо g = v^2/R, а в правой – градиент потенциала.
Именно это и указано, скажем, в БСЭ (Большая Советская Энциклопедия). Движение к истине продолжается.

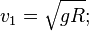

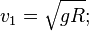

 ... может 11.2 км\с, и назовем второй (параболической) космической скоростью "убегания"
... может 11.2 км\с, и назовем второй (параболической) космической скоростью "убегания" 
