| Цитата |
|---|
BETEP IIEPEMEH пишет:
Извините, Костя, но я не понял вопроса. |
Совершенно нет необходимости извиняться.
Будь на форуме побольше людей от науки способных понять, что они не понимают вопроса - идиллия бы была в общении «наука и жизнь», а не нынешняя куча-мала.
Виноват всегда тот, кто задает вопрос (=вопросник). А ответчик никогда не должен стесняться «привести к вменяемости» вопросника.
Начинать отвечать на непонятый вопрос = изначально тратить время обоих собеседников, плюс склока и обиды.
| Цитата |
|---|
BETEP IIEPEMEH пишет:
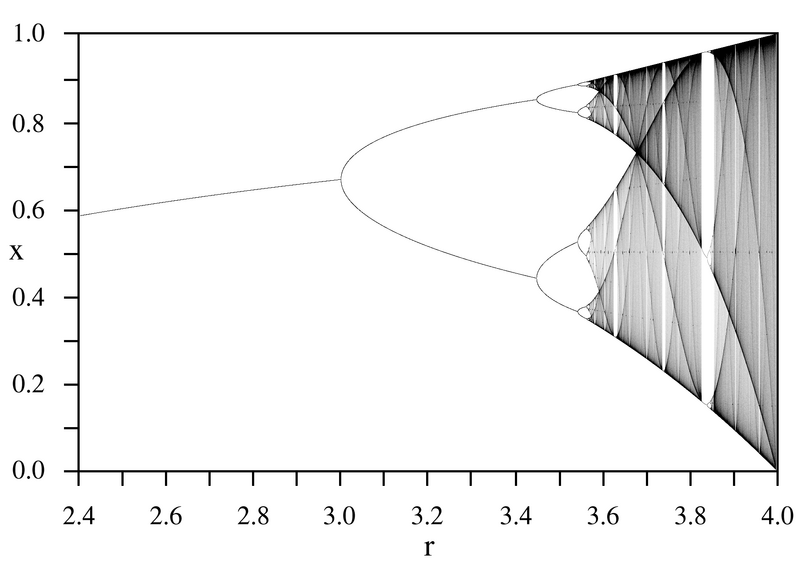
Я подозреваю, что Вы меня хотите спросить о такой вот картинке,... |
Подозреваете совершенно верно.
Я еще вначале хотел уточнить, что под скачком понимаю: «растет ветка на дереве, потом бац! и разделилась на две ветки...» но... не стал детализировать, посчитал что Вы и так поймете.
Так что Ваша картинка (график) 100% отражает то НАЧАЛО разговора, которое я и подразумевал.
Переформулирую и упрощу...
вопрос: Математической логикой выведена формула,
описывающая принцип роста веток на деревьях, и, на основе этой формулы, наука сделала предположение, что найдена причина явления «хаос превращается в порядок»?
Не стесняйтесь сообщить, если опять непонятно. Наш идеальный ход разговора - это просто ответы «да, да, да...» с Вашей стороны.
(и не надо тратить Ваши силы и время на «объяснить», продуктивнее будет если Вы подкорректируете-переформулируете вопрос ЗА меня

)
| Цитата |
|---|
BETEP IIEPEMEH пишет:
Нет, в калейдоскопе все гораздо проще - там имеет место дискретная симметрия, благодаря которой просто кусочки камушков складываются в красивую картинку. К самой теме "хаоса" это не имеет отношения. |
Ветер, да понимаю я в общих чертах ВСЁ ТО, ЧТО именно Вы сможете сказать по этой теме. Зачем нам тратить время на известное обоим?
А то, о чём я тут хотел говорить: заменить «физические камушки» на «информационные камушки» + вращать «калейдоскоп» с околосветовой скоростью, и эффекты которые возникают при этом.... ну не найдем мы тут общего языка.
Давайте замнем для ясности с калейдоскопом.
Не подумайте только, что я память Алана Тьюринга хотел как-то очернить этим диспутом. Вовсе нет. (хотя, надо признать, узнал из фильма неизвестные мне ранее подробности его личной жизни, и... вспомнил что знал о личной жизни Ньютона и некоторых других Великих... впрочем, это уже совсем другая тема разговора, типа «Кто может двигать фундамент науки, и кто его двигать не может в принципе»)


 )
)

