
№06 2025
|
Математические досуги
Если самое маленькое девятизначное число с разными цифрами 123456789 умножить на 2, 4, 5, 7, 8, то в каждом случае получится тоже девятизначное число с разными цифрами. |
|

№04 2025
|
Задачи с домино
Косточки домино, расположенные горизонтально, будем рассматривать как двузначные числа. Разместите все 28 косточек комплекта домино в 7 рядов по 4 косточки. |
|

№04 2025
|
2025 и другие квадраты
Число 2025 является, как говорят в математике, полным, или точным, квадратом, потому что оно равно квадрату числа 45. |
|
|
|
|

№11 2024
|
297 х 210 мм
В заголовке — размеры листов бумаги формата А4, которая, как правило, используется в принтерах и копировальной технике. Но почему именно такие «странные» значения? |
|

№09 2024
|
Электронное табло
Уличное электронное табло одновременно показывает 3 параметра: дату, время и температуру воздуха. |
|
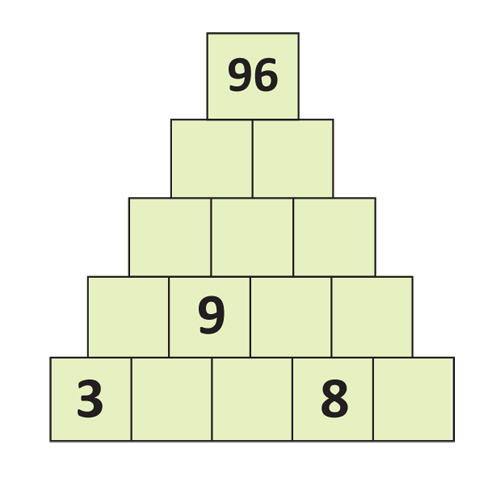
№07 2024
|
Математические досуги
В каждой строчке цифровой пирамиды числа возрастают слева направо. Сумма двух чисел, стоящих рядом в одной строке, равна числу, стоящему над этими двумя числами. |
|
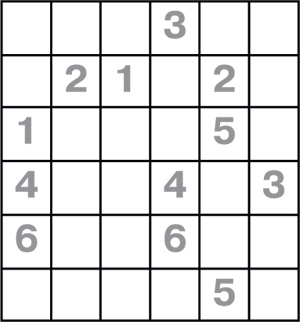
№04 2024
|
Математические досуги
Разделите квадрат 6 x 6 на шесть фигур, равных по площади, но разных по форме. Одинаковые цифры принадлежат одной и той же фигуре. |
|
№03 2024
|
Парадоксы «кроличьей норы»
Что случится, если упасть в туннель, проходящий Землю насквозь через её центр? Этим вопросом люди начали интересоваться, наверное, с момента, когда поняли, что планета круглая. |
|

№03 2024
|
Математические досуги
На листе бумаги написали все натуральные числа от 1 до 99 без промежутков. Получилось огромное число: 123456789101112…96979899. |
|
№01 2024
|
Число года 2024
Используя как можно меньше одинаковых цифр и любые математические символы и знаки действий, получить число 2024. Цифры можно группировать в числа. |
|
|
|

№09 2023
|
Число года 2023
Попробуйте отыскать различные способы представления числа 2023. |
|
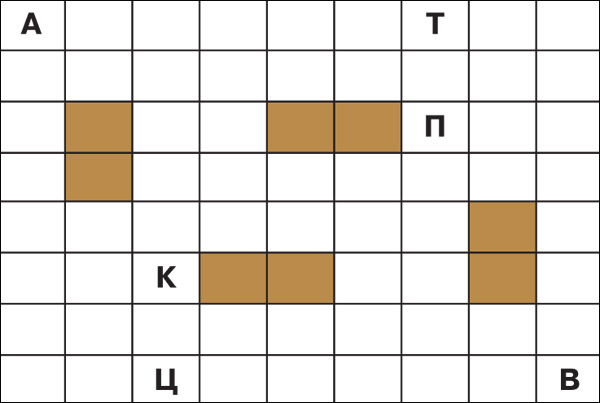
№02 2023
|
Математические досуги
Прямоугольный дачный участок поделён на квадраты. В квадрате А стоит дачник. Он должен пройти по всем квадратам. |
|

№10 2022
|
Числа на окружностях
Расставьте числа от 1 до 6 в квадратах таким образом, чтобы сумма чисел, размещённых на каждой из окружностей, была одной и той же. |
|

№08 2022
|
Необычный маршрут
Человек вышел из точки А и прошёл 1 м на юг, 2 м — на запад, 4 м — на север, 6 м — на восток, 7 м — на юг, 8 м — на запад, 10 м — на север, 12 м — на восток, 13 м — на юг, 14 м — на запад, 16 м — на север, 18 м — на восток и т. д. |
|
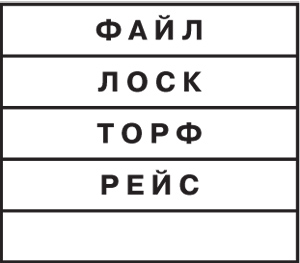
№07 2022
|
Математические досуги
Найдите закономерность в написании этих слов и впишите нужное слово в нижнюю строку. |
|

№06 2022
|
Алиса и системы счисления
В знаменитой книге Льюиса Кэрролла «Алиса в Стране чудес», во второй главе есть эпизод, когда Алиса пробует вспомнить то, что знала раньше |
|
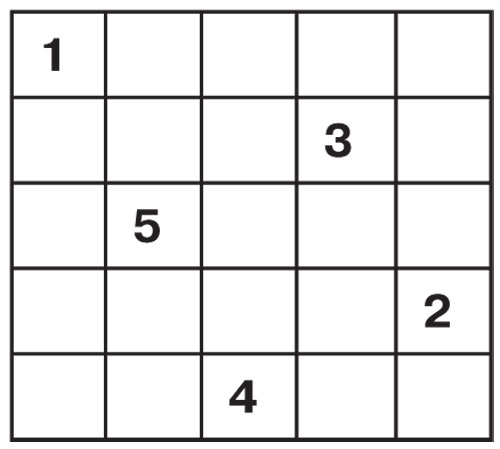
№04 2022
|
Математические досуги
Расставьте в клетки квадрата числа 1, 2, 3, 4, 5 так, чтобы в каждой строке, каждом столбце и двух диагоналях были разные числа. Некоторые числа уже стоят на своих местах. |
|

№03 2022
|
Найдите число
Есть искомое пятизначное число. При делении искомого числа на 2 получается остаток 1, при делении искомого числа на 3 получается остаток 2, при делении искомого числа на 4 получается остаток 3... |
|

№01 2021
|
Геометрия в стиле да Винчи
Один историк искусства как-то посетовал на то, что Леонардо да Винчи тратил талант и время на многочисленные рисунки, увлёкшись своей «геометрической игрой». |
|

№12 2020
|
О чём умолчали классики
Давайте перечитаем знакомые произведения русских писателей и рассмотрим их с точки зрения математики: выясним, какова скрытая мораль басни «Квартет», узнаем, далеко ли до края земли, и убедимся, что кот из лукоморья в самом деле учёный. |
|
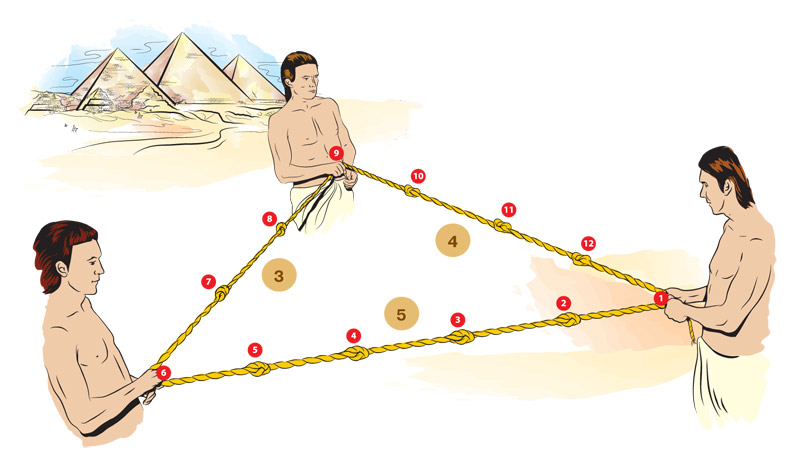
№09 2020
|
О суммах квадратов и кубов
История, о которой пойдёт речь, начинается с теоремы Пифагора, а заканчивается одним математическим открытием, сделанным в сентябре 2019 года. |
|

№07 2020
|
«Кенгуру» для всех-всех-всех
Чтобы перестановкой двух цифр получить из числа 2019 как можно бoльшее число, надо поменять местами цифры 2 и 9. |
|
|

№03 2020
|
Вопросы на засыпку
В 1920-е годы советский писатель и этнограф Тихон Захарович Сёмушкин отправился в свою первую экспедицию на Чукотский полуостров. |
|

№02 2020
|
Пути и маршруты
Знаете ли вы, что подтолкнуло английского математика Леонарда Эйлера к созданию основ теории графов? |
|
|

№10 2019
|
Измеряя круг
Преобразование круга в равновеликий ему квадрат, или квадратура круга, — самая знаменитая задача на построение из наследия древнегреческих математиков. |
|