Первая олимпиада. Математика (письменно) - 27 марта в 14.00; физика (устно) - 31 марта в 13.00. Регистрация участников 21 и 22 марта с 15 до 18 часов
Вторая олимпиада. Математика (письменно) - 16 мая в 14.00; физика (устно) - 20 мая в 11.00. Регистрация участников 10 и 11 мая с 15 до 18 часов.
Регистрация проводится на физическом факультете МГУ. Необходимо подать заявление, приложив к нему две фотокарточки размером 3x4 см, справку из школы, подтверждающую, что абитуриент обучается в выпускном классе (на выпускном курсе), или документ о среднем (полном) образовании. При себе необходимо иметь паспорт либо документ, его заменяющий.
Победители каждой олимпиады определяются по сумме полученных баллов. Результаты победителей засчитываются в качестве вступительных испытаний по физике и математике. В качестве оценки по русскому языку и литературе победителям олимпиад может быть засчитана оценка из документа о среднем (полном) образовании. В олимпиадах принимают участие учащиеся выпускных классов средних общеобразовательных учебных заведений и студенты выпускных курсов средних профессиональных учебных заведений, а также лица, имеющие документ о среднем образовании.
Настоящей статьей журнал начинает публикацию задач, предлагавшихся на олимпиадах и вступительных экзаменах по физике на физическом факультете МГУ им. М.В.Ломоносова в последние годы. При проведении вступительных испытаний особое внимание уделяется выяснению понимания сущности физических законов и явлений, умению истолковать смысл используемых понятий и применять теоретический материал к решению конкретных задач. В связи со сказанным, при разборе решений мы будем уделять особое внимание предположениям, которые необходимо сделать в ходе решения (в том числе и так называемым "стандартным предположениям", часто даже и не формулируемым в явном виде), и обоснованию возможности применения того или иного закона. Хотя общих рецептов решения задач нет, все же можно высказать ряд советов, которых следует придерживаться.
1. Внимательно прочитав условие задачи, постарайтесь сделать рисунок, отобразив на нем заданные и искомые величины. Это поможет лучше понять условие и сформулировать те дополнительные предположения, при которых будет решаться задача. Из всех возможных предположений следует выбирать приводящие к наиболее простому решению. Естественно, все они должны быть четко указаны и обоснованы. Обычно при решении задач вместо анализа движения в произвольном направлении рассматривают, пользуясь принципом независимого сложения движений, движения проекций интересующих тел на взаимно ортогональные направления. Например, так поступают, решая задачи на свободное падение тел. Часто, особенно в задачах кинематики, оказывается, что для решения целесообразно выбрать вспомогательную систему отсчета, где рассматриваемое явление описывать значительно проще, чем в той, которая либо указана прямо, либо явно подразумевается в условии. Конечно, решив задачу, окончательный ответ необходимо дать в исходной системе отсчета. Следует помнить, что законы кинематики формулируются во всех системах отсчета одинаковым образом. При решении же задач, относящихся к другим разделам, нужно использовать только инерциальные системы, так как программа вступительных экзаменов не предусматривает умения абитуриентами решать задачи этих разделов в неинерциальных системах.
2. Задачу лучше решать в общем виде, то есть используя буквенные, а не числовые значения заданных величин (соблюдая, конечно, разумную степень обобщения). При этом следует стремиться выбирать обозначения так, чтобы они "говорили" сами за себя, но все-таки полезно указывать, что понимается под той или иной введенной величиной. Полученный в общем виде ответ проверяйте не только с точки зрения размерности, но и с точки зрения так называемых предельных случаев: выбирая особые значения входящих в ответ величин, можно подобрать их так, чтобы ответ стал очевидным без решения задачи. Часто ответ должен обладать определенной симметрией, то есть не должен изменяться при замене нумерации тел. Только после таких проверок целесообразно подставлять в полученное выражение заданные числовые значения с учетом их единиц измерения. Такая последовательность при решении задач позволяет резко сократить объем арифметичес ких вычислений и тем самым не только сэкономить время, но и уменьшить вероятность арифметических ошибок, которые, как показывает опыт, обычно трудно обнаружить, в особенности в экстремальных условиях. При этом расчеты следует проводить, учитывая точность исходных данных и возможные систематические ошибки, обусловленные сделанными в ходе решения задачи допущениями. Если же числовые значения заданных величин не указаны, то необходимо выяснить их допустимые значения.
Задача 1 (1992 г.). Положив на наклонную плоскость небольшую шайбу, ее толкнули так, что она начала двигаться вверх по плоскости со скоростью υ0 = 10м/c, направленной перпендикулярно горизонтальной прямой, лежащей в этой плоскости, и за первые τ= 6c прошла путь L = 26м. Найти ускорение a шайбы, считая ее движение равнопеременным.
Решение. Из условия задачи следует, что после начала движения (t = 0) скорость шайбы и ее ускорение направлены в противоположные стороны. Следовательно, движение шайбы должно быть прямолинейным. Если выбрать ось ОХ совпадающей со скоростью шайбы в начальный момент и начало отсчета вдоль этой оси совместить с начальным положением шайбы, то координата шайбы в момент времени t должна быть равна x(t) = υ0t - at2/2, так как ускорение шайбы постоянно, а его проекция на выбранную ось отрицательна. При этом, вообще говоря, возможны два случая: 1) шайба в течение всего времени t движется только вверх, то есть υx(τ) = υ0 - aτ ≥ 0, и 2) в некоторый момент времени 0 < t1 < τ шайба останавливается, а затем начинает двигаться вниз. Этот момент времени можно найти из условия: υx (t1) = 0. Вспоминая закон изменения скорости при равнопеременном движении, получим t1 = υ0/a. Отметим, что в обоих случаях закон изменения координаты от времени имеет один и тот же вид. В большинстве действующих школьных учебников по физике термин "путь" определяется как расстояние, пройденное телом за все время движения. Такая трактовка этого термина предполагается и в программе вступительных экзаменов. Поэтому в первом из указанных случаев должно иметь место равенство x (τ) = L и, следовательно,
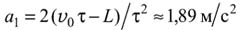 .
.
Во втором случае после момента времени t1 координата х будет уменьшаться, а путь по-прежнему будет увеличиваться. Следовательно, во втором случае
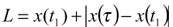 .
.
Поскольку в рассматриваемом случае шайба после момента времени t1 должна двигаться вниз по наклонной плоскости, то x (τ) < x (t1). Поэтому предыдущее соотношение эквивалентно уравнению
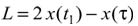
или 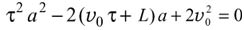 ,
,
так как по условию a 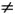 0. Корни последнего уравнения, определяемые выражением
0. Корни последнего уравнения, определяемые выражением
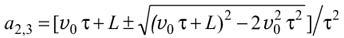 ,
,
равны 2 и 2,78 м/c2. Таким образом, при заданных значениях начальной скорости, времени движения и пути возможны три значения ускорения: 1,9; 2,0 и 2,8 , причем первое и последнее значения являются приближенными.
Задача 2 (1997 г.). Двигаясь равнопеременно, брусок проходит расстояние между точками А и В со средней скоростью υ0, причем в точке А его скорость на величину ∆υменьше, чем в точке В. Найти скорость бруска в точке С его траектории, расположенной между точками А и В и отстоящей от точки А на часть длины участка АВ.
Решение. Решение этой задачи, как и предыдущей, требует точного знания определений основных кинематических величин и понятий. Напомним, что, говоря о характере движения протяженного тела как целого, речь ведут о характере движения его центра масс. Если при этом не указывается направление, то имеют в виду характер зависимости от времени траекторной координаты, то есть вид закона движения (в узком смысле). При этом траектория может быть как прямолинейной, так и криволинейной. По определению, движение называют равнопеременным, если зависимость траекторной координаты от времени является квадратичной. При этом проекция скорости - вектора мгновенной линейной скорости на положительное направление касательной к траектории (траекторная скорость) - линейная функция времени, а быстрота ее изменения (тангенциальная составляющая ускорения) не зависит от времени.
Пусть длина участка траектории между точками А и В равна L и начало отсчета времени (t = 0) соответствует моменту нахождения центра масс бруска в точке А. Тогда, обозначив моменты времени, в которые центр масс бруска находился в точках С и В, tС и tB, согласно сказанному и условию задачи должны быть справедливы следующие соотношения:
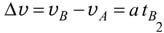 ,
,
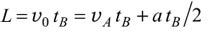 .
.
Из этих соотношений следует, что
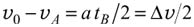
или
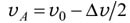 .
.
Поэтому
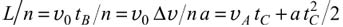 .
.
Решая последнее уравнение относительно момента времени tС, и учитывая, что в соответствии со сказанным выше tС > 0, получим
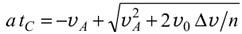 .
.
Следовательно, искомая скорость
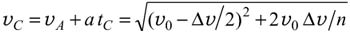 .
.
Задача 3 (1998 г.). У мальчика, сидевшего на расстоянии R от оси на вращавшейся с угловой скоростью ω карусели, выпали из кармана с интервалом времени τ два камушка. На каком расстоянии друг от друга ударились эти камушки о землю, если высота, с которой они упали, была равна h?
Решение. Поскольку камушки выпали из кармана, а не были выброшены
из него, можно считать, что начальные скорости камушков относительно земли были
равны скоростям тех точек карусели, в которых они находились в моменты выпадения.
В условии задачи дано лишь расстояние между мальчиком и осью вращения карусели,
но ничего не говорится о размерах мальчика. Вместе с тем ясно, что начальная скорость
камушков при сделанном предположении зависит от удаления камушков от оси вращения.
Будем считать, что размеры мальчика достаточно малы по сравнению с R, а
потому величину начальной скорости камушков можно считать равной υ = ωR. Поскольку высоты
падения камушков одинаковы, можно считать, что мальчик двигался по окружности,
расположенной в горизонтальной плоскости. Следовательно, начальные скорости камушков
были направлены горизонтально. Если, как это обычно и делается при решении задач
кинематики, пренебречь влиянием воздуха на камушки, то следует считать, что после
выпадения они совершали свободное падение, а потому их ускорение было равно ускорению
свободного падения g. Используя принцип независимого сложения движений
и учитывая, что по вертикали камушки должны были переместиться на расстояние h,
из закона равнопеременного движения определим время падения: 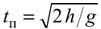 . За это время в
горизонтальном направлении, двигаясь равномерно, камушки должны были переместиться
на расстояние L = υtп. На рис. 1 пунктирными линиями показаны проекции траекторий камушков
на горизонтальную плоскость, а сплошными жирными линиями - оси лабораторной системы
координат, которую будем использовать для решения задачи. Точки 1 и 2 соответствуют
положениям камушков в моменты их выпадения. Из рисунка и сказанного ранее следует,
что первый камушек упал на землю в точке с координатами x1 = L, y1 = R. Поскольку за время
τ карусель, вращавшаяся с постоянной угловой скоростью ω, повернулась на
угол α = ωτ, то координаты точки падения второго камушка должны быть равны
. За это время в
горизонтальном направлении, двигаясь равномерно, камушки должны были переместиться
на расстояние L = υtп. На рис. 1 пунктирными линиями показаны проекции траекторий камушков
на горизонтальную плоскость, а сплошными жирными линиями - оси лабораторной системы
координат, которую будем использовать для решения задачи. Точки 1 и 2 соответствуют
положениям камушков в моменты их выпадения. Из рисунка и сказанного ранее следует,
что первый камушек упал на землю в точке с координатами x1 = L, y1 = R. Поскольку за время
τ карусель, вращавшаяся с постоянной угловой скоростью ω, повернулась на
угол α = ωτ, то координаты точки падения второго камушка должны быть равны
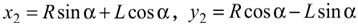 , .
, .
Учитывая, что искомое расстояние между точками падения камушков на землю
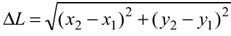 ,
,
после преобразований получим
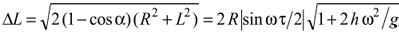 .
.
Задача 4 (1999 г.). Ведущая шестерня радиуса R вращается с постоянной угловой скоростью 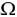 и приводит во вращение шестерню радиуса r. В некоторый момент времени метки А и В, выбитые на шестернях, совпадают (рис. 2). Через какой минимальный промежуток времени относительная скорость меток станет равной нулю?
и приводит во вращение шестерню радиуса r. В некоторый момент времени метки А и В, выбитые на шестернях, совпадают (рис. 2). Через какой минимальный промежуток времени относительная скорость меток станет равной нулю?
Решение. Поскольку проскальзывание ведомой шестерни относительно ведущей не может иметь места, то в системе отсчета, в которой оси шестерен неподвижны, модули линейных скоростей меток должны быть равны, а угловая скорость вращения ведомой шестерни ω должна удовлетворять условию 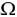 R = ωr. Следовательно, относительная скорость меток будет равна нулю в те моменты, когда векторы скоростей этих меток будут параллельны и одинаково направлены. Учитывая, что векторы скоростей меток перпендикулярны радиусам ОА и оВ (рис. 3) и шестерни вращаются во взаимно противоположных направлениях, можно утверждать, что к интересующему моменту времени t сумма углов поворота радиусов ОА и оВ должна стать равной 2
R = ωr. Следовательно, относительная скорость меток будет равна нулю в те моменты, когда векторы скоростей этих меток будут параллельны и одинаково направлены. Учитывая, что векторы скоростей меток перпендикулярны радиусам ОА и оВ (рис. 3) и шестерни вращаются во взаимно противоположных направлениях, можно утверждать, что к интересующему моменту времени t сумма углов поворота радиусов ОА и оВ должна стать равной 2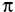 , то есть искомый промежуток времени должен удовлетворять соотношению
, то есть искомый промежуток времени должен удовлетворять соотношению
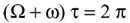 .
.
Отсюда получим
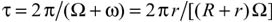 .
.
Задача 5 (1995 г.). Равносторонний треугольник АВС движется так, что в некоторый момент времени скорость вершины В равна υВ и направлена вдоль стороны АВ, а скорость вершины С направлена вдоль стороны СВ. Найдите величину скорости вершины А в этот момент времени.
Решение. Пусть для определенности скорость υB вершины В направлена так, как показано на рис. 4. Поскольку треугольник следует считать твердым телом, проекции скоростей двух любых его точек на прямую, соединяющую эти точки, должны быть равны, так как по определению расстояние между точками твердого тела не может изменяться. Следовательно, скорость υC вершины С, направленная по условию вдоль стороны СВ, должна быть равна проекции скорости вершины В на эту сторону, то есть равна υBCB. Рассуждая аналогичным образом, можно доказать, что проекция υAAB скорости вершины А на сторону АВ должна быть равна υB, а на сторону АС - υCAC. Поскольку данный треугольник является равносторонним, то углы при его вершинах равны 60°. Поэтому
. 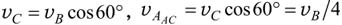
Пусть угол между векторами υА и υAABравен aα. Тогда, обратившись к рис. 4, можно доказать, что угол между векторамиυА и υAAC равен 12o - α,
и 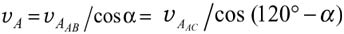 .
.
Последнее соотношение эквивалентно уравнению
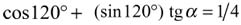 .
.
Отсюда следует, что cosα = 2/√, а искомая скорость вершины А равна 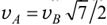 .
.
Эту задачу можно решить и другим способом, используя понятие мгновенной оси вращения. Напомним, что перемещение твердого тела за достаточно малый промежуток времени всегда можно представить как вращение вокруг неподвижной оси. Правда, в следующий момент времени при произвольном движении такой осью будет уже другая прямая. В связи с этим указанную ось и называют мгновенной осью вращения. Поскольку векторы скоростей точек твердого тела при его вращении перпендикулярны радиусам вращения, то точка пересечения мгновенной оси вращения с плоскостью, в которой лежат траектории точек треугольника , - полюс вращения - находится в точке О пересечения перпендикуляров к векторам скоростей вершин В и С, проведенных из этих вершин. Нахождение полюса вращения показано на рис. 5. Если длину стороны треугольника обозначить b, то, используя рис. 5, можно доказать, что радиус вращения вершины В равен RB = b/cos30o, а вершины А -
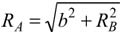
Учитывая, что угловые скорости всех точек треугольника в данный момент одинаковы (мы считаем треугольник твердым телом), используя написанные соотношения, получим
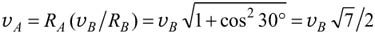 .
.
Из сказанного очевидно, что второе решение является менее трудоемким. Отметим и то, что, пользуясь понятием мгновенной оси вращения, легко ответить и на вопрос: где находятся точки, скорости которых в данный момент составляют заданный угол со скоростью вершины В, и каковы величины скоростей этих точек. Очевидно, ответить на этот вопрос, не используя мгновенную ось вращения, будет довольно сложно. Вместе с тем следует подчеркнуть, что при нахождении ускорений точек твердого тела нельзя считать ускорения точек, лежащих на мгновенной оси вращения, равными нулю.
Задача 6 (2000 г.). На цилиндрическую часть катушки радиуса r, лежащей на столе, намотана легкая нерастяжимая нить, отрезок АВ которой горизонтален (рис. 6). В момент времени t = 0 точку нити А начинают тянуть с постоянным горизонтальным ускорением. При этом катушка начинает двигаться без проскальзывания так, что ее ось не изменяет своей ориентации. Через какое время длина горизонтального участка нити изменится в n раз, если длина отрезка АВ до начала движения была L0, а внешний радиус катушки равен R?
Решение. По условию задачи при перемещении точки нити А катушка движется по плоскости, сохраняя ориентацию своей оси. Следовательно, считая, как это обычно и делается в подобных задачах, катушку твердым телом, ее движение можно представить как сумму поступательного движения со скоростью υО, равной скорости движения оси катушки, и вращения с угловой скоростью ω вокруг этой оси. Поскольку качение катушки происходит без проскальзывания, то ω = υ0/R. Из сказанного следует, что в тот момент, когда скорость оси катушки равна υО, величина скорости точки В должна быть равна
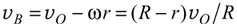 ,
,
а потому при движении катушки с течением времени длина горизонтального отрезка нерастяжимой нити должна уменьшаться.
Учитывая, что по условию задачи отрезок нити АВ остается горизонтальным и первоначально покоившуюся точку А перемещают с постоянным ускорением а, коллинеарным нити, искомый промежуток времени τ должен удовлетворять уравнению
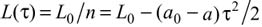 ,
,
где a0 aR/(R - r) - ускорение центра катушки.
Из этих уравнений следует, что
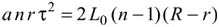
и так как 0≤, интересующий промежуток времени равен
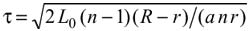 .
.




