Внимание гостей Всемирного интеллектуального фестиваля "Научно-технический прогресс - поколению XXI века" неизменно привлекал любопытный экипаж, привезенный сотрудниками Политехнического музея (см. "Наука и жизнь" № 9, 1998 г.). Это были качели, смонтированные на четырехколесной тележке. Раскачиваясь, пассажир приводит экипаж в движение, и он рывками, но довольно быстро движется в одну сторону - либо вперед, либо назад.
В чем же дело? Ведь на первый взгляд его поведение нарушает законы механики: в замкнутой системе центр масс должен оставаться на месте, а тележка, следовательно, - только совершать колебания вперед - назад возле точки равновесия. Тем не менее экипаж движется без нарушения законов сохранения, показывая, что и хорошо знакомая механика может преподносить сюрпризы.
Экипаж, который и сейчас демонстрируется в отделе игровой техники "Игротеха" Политехнического музея, не что иное, как маятник на подвижном основании. В качестве физического прибора он может стать хорошим пособием при изучении основ механики: законов превращения энергии и сохранения импульса. А в виде качелей на колесах он дает возможность, следуя наставлениям Горация - "соединяй приятное с полезным", - совместить ученье с развлечением.
Наиболее интересен в таком экипаже парадоксальный характер его перемещения. Движущий импульс, на первый взгляд, отсутствует, сцепление колес с дорогой - тоже. Экипаж представляет собой замкнутую систему, то есть такую, в которой действуют только внутренние силы. Количество движения, или импульс (произведение массы на скорость), такой системы должно сохраняться постоянным. И какие бы силы ни действовали внутри системы, как бы ни двигались отдельные ее части, центр масс всей системы должен быть неподвижным. Неподвижное орудие при выстреле испытывает отдачу и откатывается назад.
При этом суммарный импульс системы пушка - снаряд сохранился, оставшись равным нулю: (MV)орудия = -(MV)снаряда. Знак минус показывает, что они движутся в разные стороны. Перебегая с носа лодки на ее корму и обратно, мы замечаем, что лодка каждый раз сдвигается в противоположном направлении, а центр масс остается на месте. Общее количество движения системы могут изменить только внешние силы. Именно поэтому Мюнхгаузен, как бы он ни тянул себя за косичку, с места не сдвинется. Вытащить его из болота сможет только кто-то посторонний.
Все это делает не совсем понятным: почему же все-таки экипаж движется пусть с переменным ускорением, но в одном направлении. Такое его поведение можно легко объяснить, рассмотрев внимательно самое начало движения, которое имеет небольшую, но очень важную особенность.
В первый момент времени тележка не просто неподвижна. Ее либо держат, либо она упирается одной парой колес в препятствие. Ребенок начинает раскачиваться, оттолкнувшись от земли или от рамы тележки, которая с землей жестко связана. При первом же взмахе качелей система приобретает потенциальную энергию, пропорциональную высоте их подъема. Вот и объяснение поведения экипажа: на него все-таки подействовали сторонние силы, изменившие импульс. Именно энергия, полученная седоком, заставляет экипаж двигаться вперед.
Но все сказанное справедливо лишь при полном отсутствии трения. В реальности же, конечно, колебания из-за трения затухают и маятник вместе с тележкой рано или поздно замрут в неподвижности. Если силы трения в осях тележки больше, чем в подвесе маятника, то еще до остановки груза маятника поступательное движение тележки постепенно перейдет в колебания относительно общего центра масс. При обратной зависимости сначала прекратит качаться маятник, а тележка некоторое время еще будет двигаться равнозамедленно. Маятник во время движения будет отклонен на небольшой угол.
Похожим образом перемещаются любые массы, связанные упругим взаимодействием и получившие извне некоторый начальный импульс. Это могут быть и два шара, соединенные пружиной, и две молекулы в химическом соединении, и цепочка атомов в кристалле. Так что даже просто толкнув рукой предмет, мы, по существу, заставляем его двигаться подобно описанному выше маятнику. Никаких колебаний при этом заметить, конечно, нельзя: слишком велика их частота.
Вернемся к качелям на колесах. Может показаться, что седок, раскачивая качели, может обеспечить безостановочное движение экипажа. Однако это, конечно, заблуждение. Энергия седока на качелях будет расходоваться на преодоление трения, увеличение амплитуды раскачиваний, но не изменит общего импульса системы. Мюнхгаузен не сумеет выбраться из болота ни дергая себя за волосы, ни подскакивая в седле.
В заключение отметим, что старт экипажа может быть произведен тремя способами:
1. Тележку держат. Седок начинает раскачиваться, и тележку отпускают.
2. Тележку не держат. Седок начинает раскачиваться, оттолкнувшись от земли.
3. Тележку не держат. Седок начинает раскачиваться, оттолкнувшись от рамы.
Первый способ подробно разобран в заметке.
Предлагаем читателям подумать, как поведет себя экипаж в остальных случаях.
Подробности для любознательных
Разберем особенности движения экипажа с качелями подробнее. Строго говоря, описание свободных колебаний замкнутой механической системы вроде таких качелей - задача довольно сложная, требующая решения системы дифференциальных уравнений, заданных в неявном виде. Но понять принцип действия законов сохранения можно и из простого графического анализа последовательных фаз такого движения.
Математический маятник массой М1 и длиной (радиусом качания) R смонтирован на тележке массой М2 = М1. Тележка может перемещаться в горизонтальной плоскости без трения. В положении равновесия центры масс маятника и тележки расположены на одной вертикали. На систему действует только сила тяжести G, которая перпендикулярна горизонтальной плоскости и поэтому не влияет на импульс тележки. Если отклонить маятник до горизонтального положения и отпустить его, груз маятника и тележка начнут колебаться в противофазе относительно центра масс, который, в соответствии с законом сохранения импульса, будет оставаться на месте.
Однако можно заставить систему двигаться и по-другому. Начало такого движения показано на рис. 1, а полный цикл представлен на схеме зависимости скорости и смещения маятника с тележкой от угла его отклонения (рис. 2а) и на графике скорости движения тележки (рис. 2б).
Введем обозначения: Vт - скорость движения тележки, Vо - скорость маятника относительно тележки, Vа - абсолютная скорость маятника относительно Земли и рассмотрим подробно динамику такого движения. Пусть тележка установлена на горизонтальной плоскости и упирается одной парой колес в неподвижное препятствие. Отклоним маятник в сторону упора, сообщив ему потенциальную энергию Wп1, и отпустим (положение I). Пока маятник опускается, тележка остается неподвижной, так как через реакцию нити F1 вес маятника прижимает колеса тележки к упору (рис. 1а).
После того как маятник пройдет положение равновесия (рис. 1б) со скоростью Vао (положение II), потенциальная энергия груза перейдет в кинетическую Wк1 = Wп1, и реакция нити F1 начнет ускорять тележку (рис. 1в). Когда груз маятника займет наивысшее, крайне правое, положение и его относительная скорость Vо упадет до нуля (положение III), кинетическая энергия маятника тем не менее равной нулю не станет. Это объясняется тем, что маятник движется вместе с тележкой и его абсолютная скорость Va равна сумме относительной скорости маятника Vо и скорости движения тележки: Va = Vо + Vт. Так как в данной точке Vо = 0, то Va = Vт, поэтому кинетические энергии маятника и тележки станут одинаковыми и равными Wк2. Но маятник будет иметь запас дополнительной потенциальной энергии Wп2. Соотношение между ними определяется законом сохранения энергии:
Wк1=Wп1 и 2 (Wк2 + Wп2)=Wп1
.
Если остановить маятник в точке наивысшего подъема, вся система в соответствии с законом сохранения импульса дальше будет двигаться с постоянной горизонтальной скоростью V2 = Vaо/2. Но так как маятник опускается, тележка продолжает ускоряться под действием силы F1, направленной по движению тележки. Потенциальная энергия маятника продолжает переходить в кинетическую энергию тележки.
Когда маятник опустится до точки равновесия, его абсолютная скорость обратится в нуль (положение IV), а тележка приобретет скорость Vт = Vао. Ее кинетическая энергия станет равна потенциальной энергии первоначально поднятого маятника. На этом процесс обмена энергиями не закончится: маятник начнет подниматься, отклоняясь влево, и реакция натяжения нити F1 начнет тормозить тележку.
При максимальном отклоненни влево (положение V) относительная скорость маятника опять равна нулю, а абсолютная равна скорости движения тележки. Соотношение энергий в системе полностью аналогично крайне правому положению маятника. Опускаясь из крайне левого положения, маятник продолжает тормозить тележку и, придя в положение равновесия с абсолютной скоростью Vао, ее остановит (положение VI). Далее весь цикл, начиная со второй фазы, повторяется. Скорость движения тележки при этом изменяется по закону синуса (рис. 2б).
Из законов сохранения импульса и энергии нетрудно найти зависимость скоростей маятника относительно тележки и самой тележки от угла отклонения маятника:
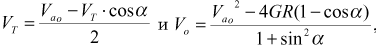
где Vт - скорость тележки; Vo - скорость маятника относительно тележки; Vао - начальная скорость маятника в момент начала движения системы; G - ускорение силы тяжести; R - радиус качания маятника; a -угол отклонения маятника от вертикальной оси. Вывод этих уравнений предоставляется сделать самим читателям.




