Оценим минимальную скорость броска, необходимую для того, чтобы камень подпрыгнул хотя бы один раз.
Если камень массой m брошен со скоростью V, то в момент удара о поверхность воды на него действуют сила тяжести Р = mg и сила реакции опоры Fр = kSV2, где S — площадь контакта камня с поверхностью воды, k — коэффициент, имеющий размерность плотности. Его величина зависит от формы камня, угла наклона плоскости камня к поверхности воды и угла между траекторией полета и поверхностью воды (угол падения α).
Если считать углы малыми, то для круглого камня радиусом r можно приближенно записать Fр = k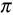
r2V2, где k 
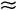500 кг/м3. Камень подскочит, если сила реакции опоры больше силы тяжести: Fp > Р. Отсюда получаем условие подпрыгивания камня: V > Vmin = √Mg/k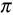r2, где Vmin — минимальная скорость броска.
Таким образом, чем тяжелее камень и чем меньше его радиус, тем с большей скоростью надо его бросать. Вот почему лучше брать довольно большие, но легкие камни. Пример. Чтобы камень радиусом 5 см и массой 100 г подпрыгнул хотя бы раз, его нужно бросить со скоростью больше 0,5 м/с (2 км/ч), камень радиусом 2,5 см и той же массой — больше 1 м/с (4 км/ч). А если взять камень радиусом 2,5 см и массой 50 г, его начальная скорость должна быть больше 0,7 м/с (2,8 км/ч).
Теперь оценим максимально возможное число подпрыгиваний камня при заданной скорости броска.
При каждом ударе о воду камень теряет энергию ∆Е (в основном за счет трения о воду), величину которой можно считать постоянной для каждого удара, так как она не зависит от скорости полета камня и определяется только его массой (по типу сухого трения). Не будет большой ошибкой предположить, что после последнего N-го удара кинетическая энергия камня станет равна 0 (хотя в действительности это не совсем так), то есть: N∆E = mV2/2.
Отсюда получаем формулу для оценки максимального числа подскоков камня: N = mV2/2∆E. Из этой формулы следует, что, бросив камень вдвое быстрее, можно учетверить количество подскоков.
Расчеты, выполненные Л. Боке, показали, что для камня радиусом 5 см и массой 100 г, брошенного так, что угол наклона его плоскости к поверхности воды α = 10°, потеря энергии при каждом ударе ∆E = 0,2 Дж. Тогда, если начальная скорость V = 6,3 м/с, максимальное число подскоков N = 10. Чтобы повторить мировой рекорд (N = 40) с помощью такого камня, надо запустить его со скоростью примерно 12,6 м/с с углом наклона 10°.
Оценим теперь, как влияет скорость вращения камня на максимальное число подскоков. Несмотря на стабилизирующее действие гироскопического эффекта, каждый удар о воду смещает положение оси вращения камня на угол δθ, приближенно равный g/rω2, где r — радиус камня, ω — скорость его вращения. Для многократного подпрыгивания необходимо, чтобы угол δθ был очень малым, то есть ω >> √g/r. Поэтому следует брать камень большого радиуса и закручивать его как можно сильнее.
После N-го удара ось оказывается смещена на угол Nδθ. Если в качестве условия полной дестабилизации положить угол смещения оси 90° – α (камень повернулся ребром к поверхности воды), то Nδθ = 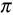/2–α, то максимальное число подскоков N = (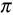/2–α)δθ. Как показали эксперименты Боке, для оценки числа подскоков достаточно положить Nδθ = 1. Отсюда N = 1/δθ = rω2/g, ω = √gN/r.
Согласно полученной оценке, для достижения мирового рекорда камень радиусом 5 см нужно закрутить со скоростью не меньше 14 оборотов в секунду (полный оборот равен 2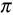 радиан). Проверьте!
Использованная литература
Bocquet L., Witkowski N. L’art des ricochets // La Recherche, № 365, 2003.
Bocquet L. Physics of stone skipping // American Journal of Physics, 2002.
См. в номере на ту же тему
А. ЗАЙЦЕВА - "Блинчики" на воде по-научному.
