«Четвёртое измерение», «параллельные миры», «гиперпространство»… Эти понятия ассоциируются у многих либо с научной фантастикой, либо с эзотерическими и мистическими трудами, авторы которых нередко спекулируют подобными терминами. Может сложиться впечатление, что для знакомства с этими понятиями требуется обладать чуть ли не сверхъестественными способностями. Однако четырёхмерное пространство вполне постижимо. Имея желание и терпение, с помощью подходов, знакомых нам ещё с уроков геометрии средней школы, можно самому заглянуть в пространства не только параллельные, но и перпендикулярные нашему трёхмерному миру. Мы предлагаем каждому попробовать представить, как выглядят четырёхмерные объекты, чтобы восхититься их красотой и гармонией. А проводником в мир четырёх измерений нам послужит одна из четырёхмерных фигур — пентатоп.
Почему пентатоп? Во-первых, потому что он — простейшая из правильных четырёхмерных фигур. Но пентатоп уникален ещё и тем, что достаточно долгое время находит себе практическое применение. Эта фигура используется в физико-химическом анализе при изучении свойств многокомпонентных систем и позволяет решать практически важные вопросы разделения сложных смесей в химической технологии.
Физико-химический анализ представляет собой комплекс методов исследования физико-химических систем, основанный на графическом построении и анализе диаграмм «состав—свойство». Его основоположником считают русского учёного Николая Семёновича Курнакова, который и применил впервые этот термин в 1913 году. По диаграмме «состав—свойство» для любой смеси веществ, находящейся в равновесном состоянии, можно найти величину какого-либо её свойства: вязкости, электропроводности, параметров кристаллической решётки. Если в роли свойства выступают температуры плавления, кипения или других фазовых переходов, то такие диаграммы называют фазовыми или диаграммами состояния. Для их построения в первую очередь необходимо графически представить состав системы во всём диапазоне концентраций её компонентов.
Смесь двух веществ можно изобразить отрезком состава, концы которого соответствуют чистым компонентам. Концентрации веществ при этом задают в виде мольных или массовых долей, которые не зависят от температуры и давления (в отличие от объёмных соотношений) и сумма которых всегда равна единице (100%). Составы смеси находят по «правилу рычага»: чем ближе точка, отражающая состав, к концу отрезка, тем больше бинарная смесь содержит соответствующего компонента. Если вторую координату, перпендикулярную отрезку состава, соотнести со значениями температуры либо давления системы, то на полученной диаграмме могут быть отражены границы плавления и кипения соответствующих смесей или пределы растворимости компонентов друг в друге. С помощью таких диаграмм можно, к примеру, рассчитать концентрации компонентов в лёгкой и тяжёлой фракциях при дистилляции, количество перегонок, необходимых для получения продукта требуемой чистоты (рис. 1), управлять процессами ректификации, кристаллизации, экстракции.
Трёхкомпонентная система уже не может быть отражена точкой на отрезке. Но добавив третью вершину, можно получить треугольник, каждая точка которого будет однозначно соответствовать одному и только одному из составов любой смеси трёх веществ по тому же правилу. Если перпендикулярно плоскости треугольника отложить координату, соответствующую температуре, то в объёме полученной треугольной призмы также можно изобразить температуры фазовых переходов и границы устойчивости смесей. На практике удобнее пользоваться изотермическими сечениями этой призмы — треугольными диаграммами для различных температур. На рис. 2 приведён пример использования треугольной диаграммы для управления процессом кристаллизации.
Легко видеть, что добавление одного компонента потребовало увеличить размерность диаграммы состояния на единицу.
Для отражения состава системы из четырёх компонентов требуется трёхмерная фигура — тетраэдр, а координате температур в трёхмерном пространстве места уже не остаётся — все три координаты заняты составом. Если для каждой температуры построить свою тетрамерным тетраэдром состава в основании и четвёртой координатой — температурой. Так что первый шаг в гиперпространство мы совершаем уже в системе из четырёх компонентов.
Пятикомпонентная система требует четвёртой координаты даже на той стадии, когда мы попытаемся графически изобразить её состав. У физикохимиков в этом случае возникает потребность в фигуре с пятью вершинами, равноудалёнными друг от друга. Это и есть пентатоп.
Пентатоп, он же правильный пятиячейник, пентахор, гипертетраэдр, 4-симплекс или «5-cell», «полиэдр {3, 3, 3}» по классификации первооткрывателя четырёхмерных фигур Людвига Шлефли, составлен из пяти тетра-эдрических элементов — «ячеек», свёрнутых в четырёхмерном пространстве так, что все они соединены друг с другом одинаковым образом. Помимо пяти «ячеек» полученная фигура имеет 10 треугольных граней, 10 рёбер и 5 вершин. Представить это наглядно можно, изобразив проекции этой фигуры на наше трёхмерное пространство и её сечения. Далее мы изучим (и для удобства изложения пронумеруем) наиболее интересные проекции пентатопа.
Сначала нам потребуется оторваться от некоторых стереотипов трёхмерного мира. Во-первых, сам трёхмерный мир потеряет свою уникальность. В пространстве четырёх измерений может существовать бесконечное множество трёхмерных пространств, которые либо пересекаются с нашим пространством под разными углами, либо параллельны ему, находясь от него на некотором расстоянии. Область пересечения трёхмерных пространств — плоскость. Трёхмерные объекты, не имея толщины по четвёртой координате, могут проецироваться в наш трёхмерный мир плоскими фигурами, если они находятся в пространствах, перпендикулярных нашему. Чем меньше угол наклона между пространствами, тем меньше искажений при проецировании. А из параллельных пространств все объекты спроецируются в наш мир без искажений.
Рекомендуем также попробовать мысленно поставить себя на место плоского «жителя Флатландии»*, который пытается постичь наш трёхмерный мир и представить тетраэдр. Трёхмерную фигуру он может изобразить на плоскости только в виде проекций, сечений и развёрток (рис. 3).
А теперь и мы попробуем шагнуть за пределы своего трёхмерного мира. Для начала изобразим развёртку пентатопа. В трёхмерное пространство эта фигура разворачивается в виде «ежа», собранного из пяти тетраэдров, один из которых — ABCD — расположен в центре (рис. 4). Четыре вершины этой развёртки, обозначенные Е1, Е2, Е3 и Е4, должны при сворачивании пентатопа, сойдясь друг с другом, образовать его пятую вершину E. Если вы попробуете без искажения объединить их в трёхмерном пространстве, то вскоре поймёте, что это невозможно.
Трёхмерные объекты в начертательной геометрии традиционно отображают на чертежах в виде трёх взаимно перпендикулярных плоских проекций. Аналогично четырёхмерная фигура имеет в прямоугольной системе координат четыре ортогональные трёхмерные проекции. Их вид определяется выбором направления координатных осей. Любой желающий может попробовать изобразить пентатоп, по-разному размещённый в системе из четырёх координат. Для этого удобно строить проекции фигуры с рёбрами единичной длины, как это делали мы. А величина неизвестных значений четвёртой координаты высчитывается по универсальному, знакомому нам ещё со школы уравнению: квадрат длины любого отрезка равен сумме квадратов его проекций.
Ещё один вариант изображения величины четвёртой координаты — это построение сечений. Так, на географических картах рельеф местности изображают изолиниями, соответствующими разным значениям её высоты. Мы будем проводить сечения пентатопа трёхмерными пространствами, параллельными нашему и отстоящими от него на разные расстояния в глубь четвёртой координаты.
Итак, начинаем изучение трёхмерных проекций пентатопа (рис. 5).
«Главная» проекция пентатопа (или проекция 1, рис. 6) наиболее проста для понимания и удобна для работы. Один из тетраэдров ABCD располагается целиком в нашем пространстве, а пятая вершина пентатопа E максимально удалена в четвёртое измерение, попадая своей проекцией прямо в центр тетраэдра. Несложно разглядеть остальные четыре ячейки-тетраэдры, уходящие в глубь четвёртой координаты. Их проекции искажены: сжаты в четыре раза, треугольными основаниями они касаются нашего пространства, а вершинами сходятся в точке E. Сечения пентатопа имеют вид правильных тетраэдров, убывающих и стремящихся к вершине E по мере удаления секущих пространств от нас по четвёртой координате (рис. 7).
В качестве примера определим четвёртую координату вершины Е, единственной из вершин этой проекции, которая находится не в нашем пространстве. Известно, что высоты единичного тетраэдра имеют величину
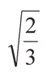
и пересекаются в точке, которая делит их в пропорции 1:3. Таким образом, отрезок DE в проекции 1 имеет длину
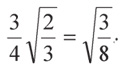
Поскольку истинная длина ребра пентатопа DE должна составлять единицу, по теореме Пифагора имеем равенство
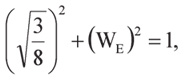
где WE — неизвестная нам величина четвёртой координаты вершины E. Отсюда получаем:
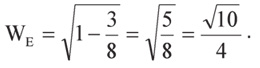
Так как в «главной» проекции тетраэдр-основание целиком находится в нашем трёхмерном пространстве, то в любой из трёх ортогонально дополняющих её проекций он будет проецироваться в плоскую фигуру, в частности в треугольник или квадрат. Такие проекции, дополняющие «главную», будут рассмотрены далее.
Проекция 2 — трижды вырожденная (рис. 8). Если две вершины пентатопа D и E расположить так, что они спроецируются в одну точку, то в той же точке выродится, то есть «исчезнет», слившись в эту же точку, одно из рёбер фигуры. Три тетраэдра-ячейки на проекции также выродятся, станут плоскими, а проекции двух оставшихся тетраэдров-ячеек совпадут друг с другом, имея вид тетраэдров, сжатых по своей высоте на 7,9% (до величины
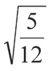
у пентатопа с рёбрами единичной длины). Единственным элементом, проецирующимся в наш мир без искажений, оказывается треугольная грань ABC, а вершины D и E имеют соответственно минимальное и максимальное значения четвёртой координаты пентатопа. Данная проекция обладает минимальным объёмом. Сечения фигуры на проекции 2 будут выглядеть как искажённые тетраэдры, сначала растущие от своей сдвоенной вершины, а потом убывающие в обратном порядке (рис. 9).
Проекция 3 — симметричная бипирамидальная (рис. 10). Эта проекция дополняет проекцию 2, как взгляд на тот же пентатоп «сбоку», из «мира четвёртой координаты». Её объём из всех проекций максимален (в 1,5 раза больше, чем у предыдущей). Не имеют искажений на этой проекции одновременно треугольная грань пентатопа ABC, объединяющая два сжатых в 1,63 раза по высоте тетраэдра-ячейки, и противолежащее ей ребро DE (ось бипирамиды), находящееся в параллельном пространстве, вокруг которого сосредоточены три остальные ячейки пентатопа, сжатые от ребра к ребру в 2,83 раза. Если сечения пентатопа в этом ракурсе начать с грани ABC, то они будут иметь вид правильных треугольных призм, растущих по высоте и убывающих по площади основания, скользящих по рёбрам фигуры вплоть до вырождения в отрезок DE (рис. 11).
Проекция 4 — в данном случае у пентатопа один из тетраэдров-ячеек ABCE вырожден (сжат) в правильный треугольник, вершины которого соединены с центром. Форма проекции — тетраэдр, слегка (на 3,2%) сжатый от вершины к основанию и имеющий высоту
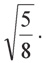(рис. 12).
Эта проекция может быть получена из «главной» проекции при замене одной из её координатных осей на четвёртую координату. Как и две предыдущие, проекция 4 имеет неискажённую треугольную грань АВС. Её плоскость в этом случае представляет собой пересечение двух взаимно перпендикулярных трёхмерных пространств: нашего и того, которое содержит в себе тетраэдр ABCE. Если разместить грань ABC в нашем пространстве и рассечь пентатоп параллельными пространствами, двигаясь вглубь по четвёртой координате, то сечения будут иметь вид пирамид, сначала усечённых, растущих к вершине D, а затем неусечённых, убывающих к наиболее удалённой от нас в гиперпространство вершине E (рис. 13).
Как было показано на рис. 3, тетраэдр может быть спроецирован на плоскость в виде квадрата. Поэтому одна из проекций пентатопа может принять форму четырёхугольной пирамиды. Эта проекция (№ 5) также может быть одной из трёх, ортогонально дополняющих «главную» проекцию.
В проекции 5 (рис. 14) одно из рёбер «сплющенного» в квадрат тетраэдра будет обладать наименьшим значением четвёртой координаты, а другое — наибольшим. Они будут проецироваться без искажений в виде диагоналей квадратного основания («сплющенного» в квадрат тетраэдра) (рис. 15).
Высота пирамиды в проекции 5 такая же, как у предыдущей проекции:
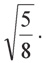
В этом случае сечения пентатопа довольно необычны. Они начинаются от одной из диагоналей квадрата и имеют вид вытянутых клинышков, которые постепенно растут вверх и уменьшаются в длину, приобретая при максимуме высоты форму правильной пирамиды, вдвое меньшей, чем вся проекция. Затем сечения начинают уменьшаться в обратном порядке, но под углом 90о, в пределе стремясь уже к другой диагонали квадрата.
Ещё одна из замечательных проекций пентатопа — дважды вырожденная, проекция 6 (рис. 16). Она имеет вид искажённого тетра-эдра, в котором два противолежащих ребра AB и CD сближены на 8,7%, а посередине одного из них расположена проекция пятой вершины E. Проекции ячеек ABCE и ABDE вырождены в треугольники и лишены объёма. По четвёртой координате пентатоп ограничен ребром AB и наиболее удалённой от него вершиной E, которая проецируется в центр этого ребра. Ребро CD по значению четвёртой координаты находится посередине, причём в пространстве, параллельном нашему (поэтому оно проецируется без искажений, сохраняя единичную длину). Сечения пентатопа начинаются из ребра AB, имея вид треугольных призм со скошенными основаниями, приобретают в максимуме своего объёма вид треугольной пирамиды с ребром CD, а после этого, имея вид пирамиды, идут на убыль, стремясь к самой удалённой от нас в гиперпространство вершине E (рис. 17). Проекция 6 может ортогонально дополнять проекции 2 и 3 при соответствующем выборе направлений координатных осей.
Кажется, пентатоп уже выдал все свои секреты, но ему ещё есть чем нас удивить — это проекция 7, которую так и хочется назвать «золотой», потому что соотношения координат пентатопа в таком ракурсе связаны «золотым сечением» — числом φ***. Эта трёхмерная проекция сама может быть спроецирована на плоскость в виде правильной пятиконечной звезды, обрамлённой пятиугольником. Изображение пентатопа на плоскости симметричным пятиугольником иногда бывает удобно при его практическом использовании — при анализе диаграмм состояния. На пентатопе состава пятикомпонентной системы в таком представлении (рис. 18) легко могут быть выделены также 5 четырёхкомпонентных систем (тетраэдры составов), по 10 трёхкомпонентных и бинарных систем (треугольники и отрезки составов соответственно) и 5 компонентов, их образующих (вершины фигуры). Их число соответствует количеству ячеек, граней, рёбер и вершин в пентатопе. В физико-химическом анализе исследования объектов начинают, как правило, от простого к сложному, определяя сначала свойства индивидуальных компонентов и бинарных смесей, переходя затем к более сложным системам. При этом каждая из более простых диаграмм состояния входит в более сложную подобно тому, как простые геометрические элементы формируют более сложные и многомерные геометрические объекты.
В проекции 7 вершины пентатопа расположены так, что расстояние от ребра AB до ребра CD в φ раз больше расстояния от ребра AB до вершины E. В трёхмерном варианте «золотая» проекция имеет вид искажённой бипирамиды с осью, смещённой в сторону одной из вершин, как промежуточная фигура между проекциями 3 и 6 (рис. 12).
Теперь, когда пентатоп нам знаком в виде своих основных проекций, можно научиться мысленно перемещать его вершины в четырёхмерном пространстве так, чтобы его проекции переходили друг в друга. Например, не меняя координат треугольника ABC и не искажая самой четырёхмерной фигуры, можно перемещать вершины D и E пентатопа так, что его проекция на наш мир будет поочерёдно принимать виды 2 — 1 — 4 — 3, а потом те же виды в обратном порядке, но перевёрнутые относительно грани ABC — как будто пентатоп «выворачивается наизнанку». Можно зафиксировать в нашем пространстве координаты ребра AB, а остальные вершины перемещать так, что ребро CD будет проецироваться в наш мир то по одну, то по другую сторону от него, а проекции будут последовательно приобретать виды 1 — 6 — 7 — 3 — 5 — 3 — 7 — 6 — 1. У проекции 5 можно, не изменяя координат вершины Е и середины двух противолежащих рёбер её квадратного основания, перемещать сразу четыре вершины пентатопа. При этом квадратное основание пирамиды сначала превратится в трапецию, а затем две вершины трапеции совместятся и мы получим проекцию 2, лежащую «на боку». Из той же проекции 5 в проекцию 2 можно попасть другим путём, через проекции 6 и 4.
При переходе проекций пентатопа друг в друга можно сохранять координаты одновременно трёх точек, а значит, и всей плоскости, которая через них проходит. Это преобразование можно назвать «вращением фигуры вокруг плоскости», которое не может быть реализовано в трёхмерном мире. Вращение пентатопа изящно изображено в анимационном ролике из Википедии (http://en.wikipedia.org/wiki/Pentatope).
Итак, как оказалось, четырёхмерное пространство для нас вовсе не закрыто. Наш многогранный проводник в мир неведомого — пентатоп — помог нам преодолеть внутренний запрет, позволил оторваться от нашего трёхмерного пространства и научил уверенно смотреть на него со стороны. Возникает резонный вопрос: в чём же практическая польза наших изысканий и как именно проекции и сечения пентатопа помогают решать задачи физико-химического анализа? Конечно, при современном уровне вычислительной техники даже исследователям, специализирующимся на анализе диаграмм состояния многокомпонентных систем, не обязательно знать про пентатоп всё то, что мы сейчас с вами узнали. Достаточно правильно составить алгоритм расчётов и задать компьютеру программу вычислений, моделируя строгими формулами то, что не удаётся постичь пространственным воображением. Тем не менее, ориентируясь в четырёхмерном пространстве, проще составить нужный алгоритм вычислений. И кроме того, эти упражнения способны доставить эстетическое удовольствие.
Всего, вместе с пентатопом, в мире четырёх измерений существует шесть платоновых*** тел. Это на единицу больше, чем в нашем трёхмерном пространстве. А вот все остальные, более многомерные пространства имеют всего лишь по три правильных фигуры: аналоги тетраэдра, куба и октаэдра. Получается, что мир четырёх измерений «богаче» по количеству правильных полиэдров, чем наш трёхмерный мир и все более многомерные пространства. Если изучение четырёхмерного пространства заинтересует читателей журнала, то можно будет рассказать про тессеракт, чаще называемый гиперкубом, и другие правильные четырёхмерные фигуры, открытые швейцарским математиком Людвигом Шлефли в середине XIX века. По мнению автора, наиболее изящна и причудлива из них фигура, состоящая из 120 додекаэдров.
Автор выражает благодарность всем друзьям, которые помогли сделать эту статью более понятной и наглядной, особенно И. В. Дуденкову, Н. В. Филимоновой, С. А. Ухову, А. А. Румянцеву, Н. В. Лазоркину и семье Нистюков.
Литература
Гарднер М. Математические досуги / Пер. с англ. Ю. А. Данилова. Под ред. Я. А. Смородинского. — М.: Мир, 1972. — 496 с. — С илл.
Перельман Ф. М. Изображение химических систем с любым числом компонентов. — М.: Наука, 1965. — 100 с.
Фёдоров П. И., Фёдоров П. П., Дробот Д. В. Физико-химический анализ безводных солевых систем. — M., 1987.
Комментарии к статье
* Страна, выдуманная английским учителем Эдвином Эбботом, жители которой обитают в двухмерном мире, не подозревая о существовании мира трёхмерного (см. «Наука и жизнь» № 11, 2007 г., статья «Есть ли «царская дорога» в математике?». Подробнее: Гарднер М. Математические досуги. — М.: Мир, 1972).
** «Золотое сечение», или «золотая пропорция», — широко и издавна используемое понятие, которое задаёт деление отрезка на такие две части, чтобы большая его часть относилась к меньшей так же, как к большей его части относится весь отрезок (a+b)/a=a/b=φ≈1,618. Традиционно считается основой красоты и гармонии. (Более подробно см. «Наука и жизнь» № 6, 2003 г., статья «Золотая пропорция. Новый взгляд»)
*** Платоново тело, или правильный многогранник, — это выпуклый многогранник, все грани которого являются равными правильными многоугольниками и в каждой вершине которого сходится одинаковое число рёбер.
