Золотую пропорцию в школе не "проходят". И когда один из авторов предлагаемой ниже статьи (кандидат технических наук В. Белянин) рассказал о золотом сечении абитуриентке, собравшейся поступать в МАДИ, в процессе подготовки к экзаменам в институт, задача неожиданно вызвала живой интерес и массу вопросов, на которые "с ходу" не было ответов. Решили искать их вместе, и тогда обнаружились тонкости в золотой пропорции, ускользавшие от исследователей ранее. Совместное творчество привело к работе, которая лишний раз подтверждает созидательные возможности молодежи и вселяет надежду, что язык науки утерян не будет.
Дж. Х. Харди
Красота математической задачи служит одним из важнейших стимулов ее нескончаемого развития и причиной порождения многочисленных приложений. Порой проходят десятки, сотни, а иногда и тысячи лет, но люди вновь и вновь находят неожиданные повороты в хорошо известном решении и его интерпретации. Одной из таких долгоживущих и увлекательных задач оказалась задача о золотом сечении (ЗС), отражающая элементы изящества и гармонии окружающего нас мира. Нелишне напомнить, кстати, что, хотя сама пропорция была известна еще Евклиду, термин "золотое сечение" ввел Леонардо да Винчи (см. "Наука и жизнь" №1, 2003 г.).
Геометрически золотое сечение подразумевает деление отрезка на две неравные части так, чтобы большая часть была средним пропорциональным между всем отрезком и меньшей частью (рис. 1).
Алгебраически это выражается следующим образом:
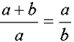 , или ,
, или , 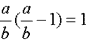
или 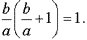 (1)
(1)
Исследование этой пропорции еще до ее решения показывает, что между отрезками a и b существуют по крайней мере два удивительных соотношения. Например, из пропорции (1) легко получается выражение,
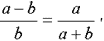
которое устанавливает пропорцию между отрезками a, b, их разностью и суммой. Поэтому о золотом сечении можно сказать иначе: два отрезка находятся в гармоничном соотношении, если их разность относится к меньшему отрезку так, как больший отрезок относится к их сумме.
Второе соотношение получается, если исходный отрезок принять равным единице: a + b = 1, что очень часто используется в математике. В таком случае
a2 - b2 = a - b = ab.
Из этих результатов следуют два удивительных соотношения между отрезками а и b:
a2 - b2 = a - b = ab,(2)
которые будут использованы в дальнейшем.
Перейдем теперь к решению пропорции (1). На практике используют две возможности.
1. Обозначим отношение a/b через . Тогда получим уравнение
x2 - x - 1 = 0, (3)
которое имеет иррациональные корни
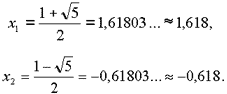
Обычно рассматривают только положительный корень x1, дающий простое и наглядное деление отрезка в заданной пропорции. Действительно, если принять целый отрезок за единицу, то, используя значение этого корня x1, получим a ≈ 0,618, b ≈ 0,382.
Именно положительный корень x1 уравнения (3) наиболее часто называют золотой пропорцией или пропорцией золотого сечения. Соответствующее геометрическое деление отрезка называют золотым сечением (точка С на рис. 1).
Для удобства дальнейшего изложения обозначим x1 = D. Общепризнанного обозначения для золотого сечения до сих пор нет. Обусловлено это, видимо, тем, что под ним понимают иногда и другое число, о чем будет сказано ниже.
Оставляемый по обыкновению в стороне отрицательный корень x2 приводит к менее наглядному делению отрезка на две неравные части. Дело в том, что он дает делящую точку С, которая лежит вне отрезка (так называемое внешнее деление). Действительно, если a + b = 1, то, используя корень x2, получим a ≈ -1,618, b ≈ 2,618. Поэтому отрезок a необходимо откладывать в отрицательном направлении (рис. 2).
2. Второй вариант решения пропорции (1) принципиально не отличается от первого. Будем считать неизвестным отношение b/a и обозначим его через y. Тогда получим уравнение
y2 + y -1 = 0 , (4)
которое имеет иррациональные корни
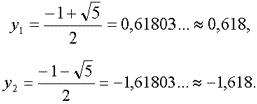
Если a + b = 1, то, используя корень y1, получим a = y1 ≈ 0,618, b ≈ 0,382. Для корня y2 получим a ≈ -1,618, b ≈ 2,618. Геометрическое деление отрезка в пропорции золотого сечения с использованием корней y1 и y2 полностью идентично предыдущему варианту и соответствует рис. 1 и 2.
Положительный корень y1 непосредственно дает искомое решение задачи, и его также называют золотой пропорцией .
Для удобства обозначим значение корня y1 = d.
Таким образом, в литературе золотую пропорцию математически выражают числом D1,618 или числом d0,618, между которыми существуют две изумительные связи:
Dd = 1 и D - d = 1. (5)
Доказано, что другой подобной пары чисел, обладающих этими свойствами, не существует.
Используя оба обозначения для золотой пропорции, запишем решения уравнений (3) и (4) в симметричном виде: = D, = -d, = d, = -D.
Необычные свойства золотого сечения достаточно подробно описаны в литературе [1-4]. Они настолько удивительны, что покоряли разум многих выдающихся мыслителей и создали вокруг себя ореол таинственности.
Золотая пропорция встречается в конфигурации растений и минералов, строении частей Вселенной, музыкальном звукоряде. Она отражает глобальные принципы природы, пронизывая все уровни организации живых и неживых объектов. Ее используют в архитектуре, скульптуре, живописи, науке, вычислительной технике, при проектировании предметов быта. Творения, несущие в себе конфигурацию золотого сечения, представляются соразмерными и согласованными, всегда приятны взгляду, да и сам математический язык золотой пропорции не менее изящен и элегантен.
Кроме равенств (5) из соотношения (2) можно выделить три интересные соотношения, которые обладают определенным совершенством, выглядят вполне привлекательно и эстетично:
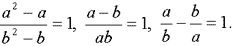 (6)
(6)
Величие и глубину природы можно ощущать не только, например, при созерцании звезд или горных вершин, но и вглядываясь в некоторые удивительные формулы, очень ценимые математиками за их красоту. К ним можно отнести изящные соотношения золотой пропорции, фантастическую формулу Эйлера eiπ = -1 (где i = √-1), формулу, определяющую знаменитое число Непера (основание натуральных логарифмов): e = lim(1 + 1/n)n = 2,718 при n → ∞, и многие другие.
После решения пропорции (1) ее идея кажется довольно простой, но, как это часто бывает со многими на первый взгляд простыми задачами, в ней скрыто немало тонкостей. Одной из таких замечательных тонкостей, мимо которой до сих пор проходили исследователи, является связь корней уравнений (3) и (4) с углами трех замечательных треугольников.
Чтобы убедиться в этом, рассмотрим, каким образом одномерный отрезок, разделенный в пропорции золотого сечения, может быть легко преобразован в двумерный образ в виде треугольника. Для этого, используя вначале рис. 1, отложим на отрезке АВ длину отрезка a дважды - от точки А в сторону точки В и, наоборот, от точки В в сторону А. Получим две точки С1 и С2, делящие отрезок АВ с разных концов в пропорции золотого сечения (рис. 3). Считая равные отрезки АС1 и ВС2 радиусами, а точки А и В центрами окружностей, проведем две дуги до их пересечения в верхней точке С. Соединив точки А и С, а также В и С, получим равнобедренный треугольник АВС со сторонами АВ = a + b = 1, АС = = ВС = a = d ≈ 0,618. Величину углов при вершинах А и В обозначим α, при вершине С - β. Вычислим эти углы.
По теореме косинусов
(АВ)2 = 2(АС)2(1 - cos β).
Подставив численные значения отрезков АВ и АС в эту формулу, получим
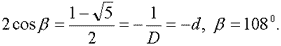 (7)
(7)
Аналогично получаем
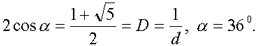 (8)
(8)
Выход золотой пропорции на двумерный образ позволил связать корни уравнений (3) и (4) с углами треугольника АВС, который можно назвать первым треугольником золотой пропорции.
Выполним аналогичное построение, используя рис. 2. Если на продолжении отрезка АВ отложить от точки В вправо отрезок, равный по величине отрезку a, и повернуть вокруг центров А и В вверх оба отрезка как радиусы до их соприкосновения, то получим второй треугольник золотой пропорции (рис. 4). В этом равнобедренном треугольнике сторона АВ = a + b = 1, сторона АС = ВС = D ≈1,618, и поэтому по формуле теоремы косинусов получаем
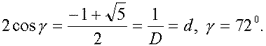 (9)
(9)
Угол a при вершине С равен 36о и связан с золотой пропорцией соотношением (8). Как и в предыдущем случае, углы этого треугольника связаны с корнями уравнений (3) и (4).
Второй треугольник золотой пропорции служит основным составляющим элементом правильного выпуклого пятиугольника и задает пропорции правильного звездчатого пятиугольника (пентаграммы), свойства которых подробно рассмотрены в книге [3].
Звездчатый пятиугольник - фигура симметричная, и в то же время в соотношениях ее отрезков проявляется асимметрическая золотая пропорция. Подобное сочетание противоположностей всегда притягивает глубоким единством, познание которого позволяет проникнуть в скрытые законы природы и понять их исключительную глубину и гармонию. Пифагорейцы, покоренные созвучием отрезков в звездчатом пятиугольнике, выбрали его символом своего научного сообщества.
Со времен астронома И. Кеплера (XVII век) иногда высказываются различные точки зрения относительно того, что обладает большей фундаментальностью - теорема Пифагора или золотая пропорция. Теорема Пифагора лежит в основании математики, это один из ее краеугольных камней. Золотое сечение лежит в основании гармонии и красоты мироздания. На первый взгляд оно несложно для понимания и не обладает значительной основательностью. Тем не менее некоторые его неожиданные и глубокие свойства постигаются только в последнее время [1], что говорит о необходимости с почтением относиться к его скрытой тонкости и возможной универсальности. Теорема Пифагора и золотая пропорция в своем развитии тесно переплетаются одна с другой и геометрическими и алгебраическими свойствами. Между ними нет ни пропасти, ни принципиальных различий. Они не конкурируют, у них разные предназначения.
Вполне возможно, что обе точки зрения равноправны, так как существует прямоугольный треугольник, содержащий в себе разнообразные особенности золотой пропорции. Другими словами, существует геометрическая фигура, достаточно полно объединяющая два математических восхитительных факта - теорему Пифагора и золотую пропорцию.
Чтобы построить такой треугольник, достаточно продолжить сторону ВС треугольника АВС (рис. 4) до пересечения в точке Е с перпендикуляром, восстановленным в точке А к стороне АВ (рис. 5).
Во внутреннем равнобедренном треугольнике АСЕ угол φ (угол АСЕ) равен 144о, а угол ψ (углы ЕАС и АЕС) равен 18о. Сторона АС = СЕ = СВ = D. Используя теорему Пифагора, легко получить, что длина катета
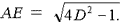
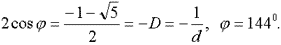 (10)
(10)
Итак, найдена непосредственная связь корня y2 уравнения (4) - последнего из корней уравнений (3) и (4) - с углом 144о. В связи с этим треугольник АСЕ можно назвать третьим треугольником золотой пропорции.
Если в замечательном прямоугольном треугольнике АВЕ провести биссектрису угла САВ до пересечения со стороной ЕВ в точке F, то увидим, что вдоль стороны АВ располагаются четыре угла: 36о, 72о, 108о и 144о, с которыми корни уравнений золотой пропорции имеют непосредственную связь (соотношения (7) - (10)). Таким образом, в представленном прямоугольном треугольнике содержится вся плеяда равносторонних треугольников, обладающих особенностями золотого сечения. Кроме того, весьма примечательно то, что на гипотенузе любые два отрезка, ЕС = D и СF = 1,0 находятся в соотношении золотой пропорции с FВ = d. Угол ψ связан с корнями D и d уравнений (3) и (4) соотношениями
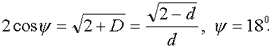 .
.
В основу представленных выше построений равнобедренных треугольников, углы которых связаны с корнями уравнений золотой пропорции, положены исходный отрезок АВ и его части a и b. Однако золотое сечение позволяет моделировать не только описанные выше треугольники, но и различные другие геометрические фигуры, несущие в себе элементы гармоничных отношений.
Приведем два примера подобных построений. В первом - рассмотрим отрезок АВ, представленный на рис. 1. Пусть точка С - центр окружности, отрезок b - радиус. Проведем радиусом b окружность и касательные к ней из точки А (рис. 6). Соединим точки касания E и F с точкой С. В результате получим асимметричный ромб АЕСF, в котором диагональ АС делит его на два равных прямоугольных треугольника АСЕ и АСF.
Обратим более пристальное внимание на один из них, например на треугольник АСЕ. В этом треугольнике угол АЕС - прямой, гипотенуза АС = a, катет СЕ = b и катет АЕ = √ab ≈ 0,486, что следует из соотношения (2). Следовательно, катет АЕ является средним геометрическим (пропорциональным) между отрезками a и b, то есть выражает геометрический центр симметрии между числами a ≈ 0,618 и b ≈ 0,382.
Найдем значения углов этого треугольника:
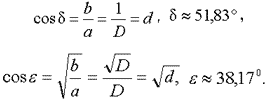
Как и в предыдущих случаях, углы δ и ε связаны через косинус с корнями уравнений (3) и (4).
Заметим, что асимметричный ромб, подобный ромбу AECF, получается при проведении касательных из точки В к окружности радиуса a и c центром в точке А.
Асимметричный ромб AECF получен иным путем в книге [1] при анализе формообразования и явлений роста в живой природе. Прямоугольный треугольник АЕС назван в этой работе "живым" треугольником, так как способен порождать наглядные образы, соответствующие различным структурным элементам природы, и служить ключом при построении геометрических схем начала развития некоторых живых организмов.
Второй пример связан с первым и третьим треугольниками золотого сечения. Образуем из двух равных первых треугольников золотой пропорции ромб с внутренними углами 72о и 108о. Аналогично объединим два равных третьих треугольника золотой пропорции в ромб с внутренними углами 36о и 144о. Если стороны этих ромбов равны между собой, то ими можно заполнить бесконечную плоскость без пустот и перекрытий. Соответствующий алгоритм заполнения плоскости разработал в конце 70-х годов ХХ века физик-теоретик из Оксфордского университета Р. Пенроуз. Причем выяснилось, что в получающейся мозаике невозможно выделить элементар ную ячейку с целым числом ромбов каждого вида, трансляция которой позволяла бы получить всю мозаику. Но самым замечательным оказалось то, что в бесконечной мозаике Пенроуза отношение числа "узких" ромбов к числу "широких" точно равно значению золотой пропорции d = 0,61803...!
В этом примере удивительным образом соединились все корни золотого сечения, выраженные через углы, с одним из случаев нетривиального заполнения бесконечной плоскости двумя элементарными фигурами - ромбами.
В заключение отметим, что приведенные выше разнообразные примеры связи корней уравнений золотой пропорции с углами треугольников иллюстрируют тот факт, что золотая пропорция более емкая задача, чем это представлялось ранее. Если прежде сферой приложения золотой пропорции считались в конечном итоге соотношения отрезков и различные последовательности, связанные с численными значениями ее корней (числа Фибоначчи), то теперь обнаруживается, что золотая пропорция может генерировать разнообразные геометрические объекты, а корни уравнений имеют явное тригонометрическое выражение.
Авторы отдают себе отчет, что высказанная выше точка зрения относительно изящества математических соотношений, связанных с золотой пропорцией, отражает личные эстетические переживания. В современной философской литературе понятия эстетики и красоты трактуются довольно широко и используются скорее на интуитивном уровне. Эти понятия отнесены главным образом к искусству. Содержание научного творчества в эстетическом плане в литературе практически не рассматривается. В первом приближении к эстетическим параметрам научных исследований можно отнести их сравнительную простоту, присущую им симметрию и способность порождать наглядные образы. Всем этим эстетическим параметрам отвечает задача, получившая название "золотая пропорция". В целом же проблемы эстетики в науке далеки от своего решения, хотя и представляют большой интерес.
Интуитивно чувствуется, что золотая пропорция все еще скрывает свои тайны. Некоторые из них, вполне возможно, лежат на поверхности, ожидая необычного взгляда своих новых исследователей. Знание свойств золотой пропорции может служить творческим людям хорошим фундаментом, придавать им уверенность и в науке и в жизни.
1. Шевелев И. Ш., Марутаев И. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. - М.: Стройиздат, 1990. - 343 с.
2. Стахов А. П. Коды золотой пропорции. - М.: Радио и связь, 1984. - 152 с.
3. Васютинский Н. А. Золотая пропорция. - М.: Молодая гвардия, 1990. - 238 с.
4. Коробко В. И. Золотая пропорция: Некоторые философские аспекты гармонии. - М. - Орел: 2000. - 204 с.
5. Урманцев Ю. А. Золотое сечение // Природа, 1968, № 11.
6. Попков В. В., Шипицын Е. В. Золотое сечение в цикле Карно // УФН, 2000, т. 170, № 11.
7. Константинов И. Фантазии с додекаэдром // Наука и жизнь, 2001, № 2.
8. Шевелев И. Ш. Геометрическая гармония // Наука и жизнь, 1965, № 8.
9. Гарднер М. От мозаик Пенроуза к надежным шифрам. - М. : Мир, 1993.




