Как развивается научная модель в естественных науках? Накапливается житейский либо научный опыт, его вехи аккуратно формулируются в виде постулатов и образуют базу модели: набор утверждений, принимаемых всеми, кто работает в рамках этой модели.
Новые исследования и добытые в них знания могут поколебать набор утверждений, принимаемых в качестве бесспорных, и, если к тому появляются основания, какие-то утверждения заменяются на новые. Например, когда на пороге ХХ века началось развитие физики в области, выходящей за пределы привычного мак-ромира, был сформулирован постулат о том, что скорость света предельна, больше её скоростей не бывает.
Постулаты реальной науки — результат большой и длительной работы по накоплению знаний. Их невозможно доказать абсолютно, но в конкретный момент они лучше всего подходят для описания наблюдаемой реальности и не вызывают явных противоречий. Если мы исходим из того, что яблоко падает с ветки на землю, а не улетает куда угодно, то мы принимаем закон всемирного тяготения, хотя доказать его в абсолютном, логическом смысле слова далеко не просто, если вообще возможно.
Теорема Гёделя — это математическое утверждение, сделанное относительно одного конкретного инструмента познания — логики.
Любую логику задают три структурных элемента: её алфавит, утверждения и правила вывода.
Алфавит — это, например, символы переменных (A, B, C…), которые принимают различные значения, и кванторы существования и общности. С их помощью можно строить утверждения, например такое: «Любой дедушка — мужчина» («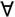
(любое) х, принадлежащее множеству Х, принадлежит также его множеству Y», где х — человек, Х — множество мужчин, имеющих внуков, а Y — множество всех мужчин).
Это утверждение является высказыванием — оно всегда либо истинно, либо ложно. Но изменим его немного: «Любой предок старше тебя на два поколения — мужчина», — и в зависимости от допустимых значений выражения «предок на два поколения старше тебя» утверждение окажется либо истинным, либо ложным. Для переменной х («предок старше на два поколения») возможно четыре значения для каждого x: две бабушки и два дедушки. Из них на множестве бабушек утверждение будет ложным, а на множестве дедушек — истинным.
Разные утверждения могут содержать одну и ту же переменную, определённую на одном и том же множестве, и истинность обоих будет одинаковым образом зависеть от её значения. Допустим, в нашем мире все мужчины любят рыбалку, а все женщины — нет, тогда утверждение «Человек любит рыбалку» истинно на множестве мужчин и ложно на множестве женщин. Иначе говоря, для любого значения переменной, при котором истинно первое утверждение, будет верно и второе.
Правила вывода позволяют конструировать из таких утверждений новые. Например, утверждение «Любой дедушка любит рыбачить» выведено из двух предыдущих, потому что любой дедушка — мужчина (по первому утверждению), а все мужчины любят рыбачить (по второму). Является ли оно истинным?
Для этого нам придётся задать себе вопрос: а что такое истинное утверждение?
Логика отвечает на него так: это утверждение, которое выводится из набора аксиом данной логики с помощью правил вывода данной логики или само является аксиомой. Иначе говоря, если, пользуясь правилами вывода, мы можем вывести из истинных утверждений какое-то новое утверждение, оно тоже будет истинно.
Но ведь, располагая алфавитом, утверждений можно составить бесконечно много. Каждое ли из них мы можем получить из аксиом с помощью правил вывода?
Этот вопрос исторически порождает много споров. Например, одну из самых затяжных полемик вызвала аксиома о параллельных прямых: выводится она из четырёх предыдущих аксиом или нет? Дело в том, что геометрию изначально строили на аксиоматике, а не на «интуитивной понятности» тех или иных объектов. Первые аксиомы геометрии утверждают, что есть точки и есть прямые; есть точки, принадлежащие данной прямой, а есть не принадлежащие; через две точки можно провести одну прямую. Существуют ещё три группы аксиом, независимые одна от другой. Пятая же звучит так: «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной». Спор о том, можно или нельзя вывести это утверждение из четырёх предыдущих, длился две с лишним тысячи лет.
Молодой венский математик Курт Гёдель задался вопросом: любое ли высказывание, возможное в данной конкретной логике, можно вывести из набора её аксиом с помощью её правил вывода? Иначе говоря, возможны ли среди утверждений такие, которые нельзя проверить на истинность (соответствие набору аксиом)?
В 1931 году он опубликовал две теоремы, математически доказав, что утверждения, созданные в конкретной логике, всегда будут одного из трёх типов: те, которые можно вывести из базового набора аксиом (истинные); такие, что можно доказать их противоречие аксиомам (ложные); и ни те, ни другие.
Лучше всего гёделевский «принцип неполноты» можно проиллюстрировать ситуацией следователя, у которого есть подозреваемый и набор фактов. Возможно, следователь откажется от своих подозрений на основании полноценного алиби. Возможно, докажет виновность подозреваемого. Но не исключено и то, что ему не хватит данных для решения, — иногда аксиоматика оказывается узка. Разумеется, её можно расширить по потребности, например дополнить ещё одной аксиомой, и что-то из неопределённого определится, но что-то всё равно останется неопределённым. Так расширить аксиоматику, чтобы ничего неопределённого не осталось, чтобы утверждения распределились без остатка на истинные и ложные, невозможно, что, собственно, и составляет логико-математическую суть теоремы Гёделя.
Однако значимость доказанного Гёделем выходит за пределы математики, потому что аппаратом логики (алфавит, аксиоматика, правила вывода) люди пользуются при построении любой научной модели. И если постулат о параллельных прямых (как и любой другой) потенциально «имеет право» не быть выводимым из четырёх аксиом геометрии, то же верно в отношении постулатов любой области знания, где модели строятся на логических основаниях. Потому что очевидное и доказуемое — не одно и то же.
