День рождения Кащея Бессмертного
Кащей Бессмертный пригласил только самого себя, потому что все перечисленные родственники - это он и есть.
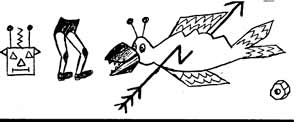
Язык первобытных роботов
На языке первобытных роботов с планеты Суперлом фразу "Я пошел на охоту" надо записать так:
Сосновый мед и воздушный шарик
Иа-Иа знает, что шарик, который надували ртом, не может полететь вверх. И уж тем более - поднять весьма упитанного, пусть и голодного Винни-Пуха.
ПРЕСТУПЛЕНИЕ В ЗАМКЕ (№ 1, 1998 г.)
Сержант Глум с удивлением посмотрел на инспектора. Но на всякий случай стал поближе к двери, чтобы отрезать слуге Айвену путь к бегству.
- В замке толстые стены, - сказал Борг, - пол закрыт пушистым ковром. Вы не могли слышать никаких "тяжелых шагов".
Для наглядности инспектор даже потопал несколько раз. Звука практически не было.
ОГРАБЛЕНИЕ КОЛЛЕКЦИОНЕРА (№ 2, 1998 г.)
- Инспектор! - простодушное лицо сержанта вытянулось от изумления. - Почему вы не верите господину Голдау?
- Потому что синяк у него под правым глазом.
- Ну и что? - хором воскликнули сержант и коллекционер.
- Если бы все было так, как рассказываете вы, господин Голдау, ваш синяк находился бы под левым глазом. Ведь мифический грабитель шел вам навстречу, зонтик из левой руки бросил уже после удара. Значит, бил правой, - попасть он должен был только в левый глаз.
В ОДНОМ УНИВЕРМАГЕ (№ 12, 1997 г.)
Из условия задачи следует, что Давыдов - не бухгалтер и не товаровед, а Васильев - не кассир и не зав. отделом, а кроме того, не бухгалтер и не товаровед. Следовательно, Васильев - продавец (остальные варианты исключены).
Теперь видно, что женихом на предстоящей свадьбе может быть только Гришин (Васильев уже женат, а Давыдов будет шафером на свадьбе). А невеста - Борисова, так как с Алексеевой у Гришина исключительно деловые отношения.
Далее можно сделать вывод, что Гришин либо бухгалтер, либо товаровед. Те же варианты относятся и к Борисовой. Раз Гришин - не кассир (а Васильев, как известно, продавец), то кассиром может быть только Давыдов. Должности кассира и продавца уже заняты, а если еще учесть, что Алексеева не может быть ни бухгалтером, ни товароведом, то будет ясно, что Алексеева - зав. отделом. А раз она жила в одной комнате с бухгалтером, понятно, что невеста - бухгалтер.
Теперь видно, что жених - товаровед и эту должность занимает Гришин, а бухгалтер - Борисова.
РЖЕВСКИЕ КУБИКИ (№ 9, 1997 г.)
Несмотря на то, что число решений головоломки - сложить из кубиков со штырьками и отверстиями три куба 2х2х2 - велико, задача оказалась не из легких. Одно сказать, что "метод тыка" - случайная подборка - не срабатывал: любое найденное решение явилось результатом логических размышлений. В числе приславших ответы нам встретились и старые знакомые, принимавшие участие еще в составлении каталога вращений Кубика Рубика (как, например, Г. И. Ярковой из г. Тольятти), и наши новые подписчики.
Прежде всего читатели, которые взяли на себя труд провести компьютерный анализ возможных вариантов решений, опровергают утверждение автора головоломки о том, что "если собраны два куба, то из оставшихся восьми кубиков всегда можно сложить третий".
Например, сложив два куба 2х2х2 из кубиков 1, 3, 4, 7, 8, 9, 14, 16 и 2, 10, 11, 12, 15, 20, 21, 24, оставшиеся кубики 5, 6, 13, 17, 18, 19, 22, 23 в куб сложить не удастся.
Полное число решений слишком велико, чтобы сосчитать его без компьютера. В. И. Кабанович сообщает: "Существует 1050466 способов разбить комплект на три восьмерки, складывающиеся в кубы. Комбинируя же различные способы сборки в куб каждой из трех восьмерок кубиков для каждого из этих разбиений (конечно, поворот куба 2х2х2 не считается новым способом его сборки), получим полное число решений головоломки - 505537942.
Интересно выделить из этого огромного числа решений небольшую группу каким-либо простым ограничением.
Можно, например, потребовать, чтобы каждый из трех кубов был сложен из восьмерки кубиков, которая складывается единственным способом. Таких решений всего 42". На рисунке одно из них.
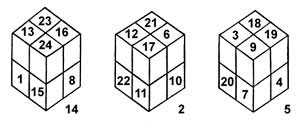
Рядом с каждым кубом записан номер дальнего кубика.
И. Константинов .




