РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ И СТАТИКИ

При решении обсуждаемых задач желательно придерживаться следующего стандартного порядка.

Нарисуйте объекты, взаимодействие которых требуется учесть, и изобразите силы, действующие на каждое из рассматриваемых тел, помня о третьем законе Ньютона (рисуйте силы парами!). При этом силы реакции, с которыми взаимодействуют соприкасающиеся твердые тела и которые обычно не известны, удобно изображать в виде двух составляющих: N, направленной по нормали к границе раздела соприкасающихся тел, и перпендикулярной ей тангенциальной F_тр, обычно называемой силой сухого трения. Такой способ изображения силы реакции обусловлен тем, что величины указанных составляющих взаимосвязаны. Согласно закону Кулона-Амона, величина силы сухого трения покоя F_тр≤μN, где μ коэффициент трения, а ее направление противоположно тому, в котором двигалось бы данное тело относительно соприкасающегося с ним в отсутствие трения. При наличии скольжения обычно полагают, что величина силы сухого трения не зависит от скорости и равна μN, хотя в действительности F_тр по мере роста скорости относительного движения может вначале уменьшаться (вплоть до двух раз), а затем, увеличиваясь, даже превысить максимальное значение силы сухого трения покоя.

Глядя на сделанный рисунок, запишите для каждого из тел уравнение движения в виде m_ia_i=ΣF _i, где ΣF_i векторная сумма всех сил, действующих на тело массой m_i, центр масс которого движется с ускорением а_i относительно инерциальной системы отсчета (ИСО). Обычно для дальнейшего решения задачи составленные векторные уравнения следует переписать в проекциях на оси декартовой ИСО. Хотя существование ИСО постулируется первым законом Ньютона, только на основании опыта удается определить, с каким реальным телом следует связать систему отсчета, чтобы ее можно было считать инерциальной.

Согласно современным данным, при исследовании движения тел в небольшой области пространства в течение нескольких минут обычные методы измерения дают результаты, согласующиеся с расчетными в пределах ошибок измерения, если инерциальной считать лабораторную систему (ЛСО), то есть систему отсчета, неподвижную относительно тех точек поверхности Земли, вблизи которых производится эксперимент. При этом силу F_гр гравитационного притяжения тела к Земле следует заменить силой тяжести F_т, под действием которой тело относительно ЛСО двигалось бы с ускорением, равным ускорению свободного падения g в той области, где производится эксперимент. Из сказанного следует, что по определению F_т=mg. Сколь сильно отличаются друг от друга F_гр и F_т по величине и направлению, зависит от географического положения интересующей области и, в первую очередь, обусловлено суточным вращением Земли и отклонением ее формы от сферически симметричной.

Если же речь идет о более масштабных движениях, например движении искусственных спутников Земли, то инерциальной обычно можно считать геоцентрическую систему, центр которой совпадает с центром Земли, а оси направлены на достаточно удаленные от Земли звезды.

Полученная указанным способом система уравнений, как правило, оказывается неполной. Запишите недостающие уравнения, учитывая кинематические связи между телами системы, особенности сил и специальные допущения. Если в задаче особо не оговариваются иные условия, то по умолчанию, без формулировки их в явной форме, обычно считают выполненными так называемые "стандартные" допущения:

при криволинейном движении размеры тел столь малы, что их можно заменить материальными точками. При прямолинейном движении считается, что тела движутся поступательно и являются твердыми;

все нити, связывающие тела, нерастяжимы и в процессе движения остаются натянутыми. Если тела соединены пружинами, то при установившемся движении натяжение пружин не изменяется и их длина остается постоянной;

участки нитей, не лежащие на блоках, при движении тел не изменяют своей ориентации относительно поверхностей, по которым движутся связанные нитями тела;

грузы по наклонным плоскостям движутся так, что их скорости перпендикулярны линии пересечения этих плоскостей с горизонтальной плоскостью;

блоки, если они вращаются при движении тел, считаются идеальными цилиндрами, вращающимися вокруг своих геометрических осей, и на них не действуют силы сопротивления движению;

действием воздуха на рассматриваемые тела, массой нитей и блоков, а также гравитационным взаимодействием тел можно пренебречь.

Следует отметить, что многие абитуриенты испытывают серьезные трудности не только при обосновании возможности применения в данной конкретной ситуации этих допущений и вытекающих из них следствий, но и при формулировке самих допущений. Это, по-видимому, связано с тем, что в школьных учебниках и пособиях для поступающих "стандартным" допущениям порой не уделяется должного внимания.

Решите полученную полную систему уравнений, обращая внимание на равносильность производимых математических преобразований и выделяя особые с точки зрения математики случаи. Часто некоторые из полученных решений не удовлетворяют возможным значениям искомой величины с точки зрения ее физического смысла и условия задачи. Ясно, что такие решения должны быть отброшены.

Проанализируйте полученные решения с точки зрения размерности и так называемых предельных случаев.

Подставьте в полученные выражения заданные числовые значения, помня о существовании разных систем единиц измерения и соблюдая разумную точность при вычислениях. Если числовые данные в условии не приведены, найдите соотношения между входящими в ответ величинами, при которых справедливо полученное решение.

Применение указанной схемы должно помочь не только избежать часто встречающихся у абитуриентов ошибок, но и быстрее получить правильный ответ. В качестве иллюстрации рассмотрим решение задач, предлагавшихся на вступительных испытаниях на физическом факультете МГУ в последние годы.

Задача 1 (1998 г.). На горизонтальной плоскости стоит гладкий клин массой М с углом α при основании. На клин положили брусок массой m, к которому прикреплена легкая нерастяжимая нить, проходящая через зажим, закрепленный на клине так, как показано на рис. 1. С каким ускорением может двигаться клин после того, как брусок отпустят без начальной скорости, если максимальная величина силы трения покоя нити о зажим равна F?

Решение. Поскольку клин по условию задачи является гладким, сила R реакции горизонталь ной плоскости, действующая на него, направлена вертикально вверх, а сила N реакции клина на брусок - по нормали к наклонной плоскости клина так, как показано на рис. 2. Здесь же изображены сила , действующая на клин со стороны бруска, и силы тяжести mg и Mg, действующие на брусок и клин. По условию задачи на нить не действуют силы тяжести. Поэтому в соответствии с рис. 1 отрезок нити между бруском и зажимом можно считать прямолинейным и параллельным наклонной плоскости клина. Поскольку со стороны нити на зажим и прикрепленный к ней брусок действуют силы, направленные только вдоль ее оси, можно утверждать, что эти силы параллельны наклонной плоскости клина и направлены так, как показано на рис. 2. С учетом обозначений, использованных на этом рисунке, и третьего закона Ньютона силы, действующие на нить со стороны зажима (T) и бруска (Т*), должны удовлетворять условиям: и . Поскольку на нить не действуют другие тела, масса нити полагается равной нулю, а ее ускорение, очевидно, может быть только величиной ограниченной, то на основании второго закона Ньютона можно утверждать, что а потому . С учетом полученных соотношений, считая, как обычно лабораторную систему XOY, неподвижную относительно плоскости, на которой стоит клин, инерциальной, уравнения движения клина и бруска в проекциях на оси этой системы можно записать в виде:

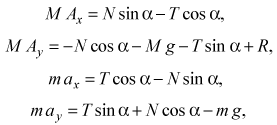
где А_х и А_у проекции ускорения А клина на оси ОХ и ОY, а_х и _ау проекции ускорения бруска на указанные оси.

Если ускорение бруска равно нулю, то из двух последних уравнений следует, что T = m g sinα . Поэтому если F ≥ T, то и брусок и клин должны оставаться неподвижными, то есть при F ≥ m g sinα ускорение клина A = 0.

Если же F < m g sinα , то сила натяжения нити Т при сделанных выше предположениях будет равна F максимальной величине силы трения нити о зажим и брусок должен скользить по клину, а клин, в свою очередь, также должен двигаться с некоторым ускорением. Поскольку клин может двигаться только горизонтально, то A_y = 0. Ясно, что отличные от нуля компоненты ускорений клина и бруска не могут быть независимыми, так как брусок по условию движется лишь по поверхности клина. В системе координат X₁О₁Y ₁, неподвижной относительно клина, оси которой параллельны осям лабораторной системы отсчета XOY, приращения координат 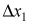и 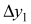некоторой точки бруска должны удовлетворять условию 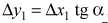. Учитывая, что начала отсчета на осях OY и O₁Y₁, показанных на рис. 2 систем координат, не смещаются по вертикали друг относительно друга при возможных перемещениях клина, можно утверждать, что 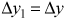. Вместе с тем, если клин испытывает перемещение 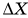, а брусок относительно клина смещается на 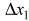, координаты точек бруска относительно оси OХ изменяются на 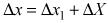. Таким образом, приращения координат клина и бруска относительно осей лабораторной системы отсчета связаны между собой соотношением 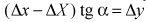.Учитывая, что полученное соотношение справедливо для любых моментов времени, когда брусок находится на клине, на основании последнего соотношения и определений скорости и ускорения в данном направлении можно утверждать, что составляющие ускорений бруска и клина, входящие в уравнения движения этих тел, связаны между собой соотношением a_y = (a_x - A_x) tg α. Из этого выражения и уравнения движения бруска следует, что

m A_x sinα = mg cos α - N/ Умножив обе части полученного соотношения на sina и сложив результат с первым уравнением движения клина, определим проекцию ускорения клина на ось ОХ при F < mg sinα:

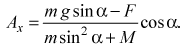
Таким образом, при выполнении сделанных в ходе решения задачи предположений проекция ускорения клина на ось ОХ равна:

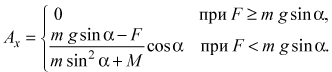
Задача 2 (1997 г.). Через гладкий блок, прикрепленный к гладкой неподвижной наклонной плоскости, образующей с горизонтом угол α, перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой М, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой m, как показано на рис. 3. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением а относительно груза. Найти силу натяжения нити.

Решение. Для решения задачи выберем неподвижную относительно наклонной плоскости систему координат XОY так, как показано на рис. 4. Будем считать, что центр масс бруска и нить лежат в одной вертикальной плоскости, перпендикулярной линии пересечения заданной наклонной плоскости с горизонтом. Поскольку нить нерастяжима, а груз после отпускания (момент времени t=0) скользит относительно нити с постоянным ускорением, то координата у бруска и координата х груза для произвольного момента времени 0 < t < t_k, где t_к момент времени, когда либо брусок хотя бы частично начнет соскальзывать с наклонной плоскости, либо груз перестанет двигаться по нити, должны удовлетворять соотношению

x + y = C + at²/2,

где С длина отрезка нити от бруска до верхней грани груза перед их отпусканием. Поэтому проекция скорости груза на ось ОХ

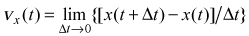
и проекция скорости бруска на ось ОY

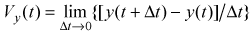
для указанных моментов времени должны удовлетворять соотношению

.

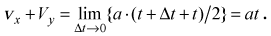Следовательно, уравнение кинематической связи - соотношение между соответствующими координатами ускорения бруска и груза - имеет вид a_x + A_y = a.

Поскольку блок гладкий, а нить невесома, то величина Т силы натяжения на всем отрезке нити от бруска до верхнего торца груза остается постоянной. Учитывая, что наклонная плоскость гладкая, и пренебрегая силами трения со стороны окружающей рассматриваемые тела среды, на основании второго закона Ньютона уравнения движения бруска и груза для указанных моментов времени можно записать в виде

m a_x = m g - T

и

M A_y = M g sinα - T,

где g величина ускорения свободного падения. Конечно, сказанное верно в предположении, что связанная с плоскостью ЛСО инерциальна.

Решая совместно уравнения кинематической связи и движения тел, найдем искомую величину силы натяжения нити при выполнении сделанных предположений:

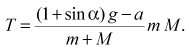
(Окончание следует.)