Возьмем произвольный номер a,b-c,d и рассмотрим три случая.
1. Среди цифр нет нулей. Составим из них два числа ab и cd (это, разумеется, не произведения). Покажем, что sin[(ab)!]° = sin[(cd)!]° = 0.
Действительно, sin(n!)° = 0, если n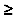 
6, так как sin(6!)° = sin720° = sin(2x360)° = 0. Любой факториал получается умножением 6! на последующие числа (например, 8! = 6!x7x8), давая кратное число раз по 360° в аргументе синуса, делая его (и тангенс тоже) равным нулю.
2. В какой-то паре цифр есть ноль. Умножаем его на соседнюю цифру, и полученный ноль приравниваем к синусу факториала в градусах, взятого от числа в другой части номера.
3. Нули в обеих частях номера при умножении на соседние цифры дают тривиальное равенство 0 = 0.
Разбиение общего решения на три пункта с умножением на ноль в пунктах 2 и 3 связано с тем, что sin(n!)°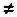 
0 при n < 6. Попутно отметим, что частное решение с использованием sin(7!), предложенное В. Донченко (см. "Наука и жизнь" № 6, 2001 г.), по существу, реализует ту же идею.
Таким образом, игра Ландау проходит и развивается двумя путями. Во-первых, идет поиск частных решений, множество интереснейших вариантов которых было предложено читателям журнала. А во-вторых, проходит не менее захватывающая работа по отысканию общих решений (естественно, что все они автоматически исключаются из игры, ибо в противном случае она теряет интерес и занимательность).
На сегодня имеется три общих решения, находящиеся в разрешенных правилами рамках элементарной математики.
1. Решение неизвестного харьковского математика, сообщенное учеником Л. Д. Ландау профессором М. Кагановым (см. "Наука и жизнь" № 1, 2000 г.). Оно содержит "архаичный" секанс и сводит любое число к числу, на единицу меньшему, позволяя в конце концов получить равенство в любой паре номеров:
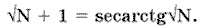
2. Решение кандидата физико-математических наук С. Федина, которое использует аналогичную идею, но обходится без устаревшего секанса (см. "Наука и жизнь" № 4, 2000 г.):
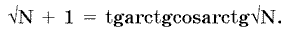
3. И, наконец, приведенное выше решение автора настоящей заметки, приводящее к цели гораздо быстрее.
Доктор геолого-минералогических наук, кандидат физико-математических наук Б. ГОРОБЕЦ.
Исследования показали, что все возможные комбинации номеров от 00 - 01 до 99 - 99 разделяются на две группы.
Номера, правые и левые части которых удается решить с помощью математических знаков +, -, :, x,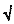 
, lg, log и символа m!.
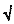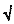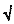Все остальные номера, правые и левые части которых приводятся с помощью упомянутых знаков к соотношениям 0 - 2, 0 - 3 и 2 - 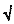3. После этого их можно уравнять с помощью универсальной формулы, сообщенной М. Кагановым, или аналогичной, полученной мною после ряда тождественных преобразований и извлечения квадратного корня:
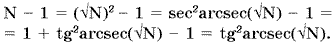
И. ДОВГАНЧУК (г. Новосибирск).
