То, что видим мы, -
Видимость только дна,
Настоящая сущность
Вещей не видна.
Омар Хайям
Экспериментальные данные о строении молекулы воды и разбиения Пенроуза
Еще в 1810 году английский физик Джон Дальтон построил из шаров и стержней модели некоторых молекул. Шары соответствовали атомам, стержни - химическим связям в молекуле. Конечно, в то время Дальтон не мог указать величину расстояний между атомами в молекуле и валентных углов. Это и сейчас составляет трудности, например для воды в жидком состоянии. Именно поэтому авторы статьи [1] пишут, что не могут экспериментально подтвердить свою гипотезу. Однако если рассматривать вещества в газообразном или твердом состоянии, то геометрические конфигурации и параметры молекул можно определить. Соответствующие данные имеются в справочниках, например, в книге Ромбиди Н. Г. и Толмачева С. М. "Таблицы стандартных и справочных данных. Геометрическая конфигурация и межъядерные расстояния молекул и ионов в газовой среде". Книга вышла в 1978 году в Издательстве стандартов .
Используя справочные данные такого рода и экстраполируя их, авторы работы [1] приходят к модели молекулы талой воды, показанной на рис. 1.
На рисунке приведены величины межъядерных расстояний (они, очевидно, одинаковы) и величина валентного угла НОН. Соединив далее вершины НН и присоединив к полученному треугольнику симметрично еще один такой же треугольник, получаем один из двух знаменитых ромбов Пенроуза (рис. 2).
На рисунке изображен ромб Пенроуза с внутренними углами 108 и 72°, разделенный диагональю на два равных треугольника. Если принять, что сторона НН = 1, то, как показано в [1], мы получаем треугольник НОН, в котором
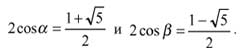
Такой треугольник в статье [2] назван первым треугольником золотой пропорции. Мы его, для краткости, назовем первым золотым треугольником.
На рис. 3 изображен еще один ромб Пенроуза с внутренними углами 144 и 36°. Заметим, что
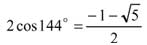
(угол при вершине В тупой и его косинус отрицательный). Как уже отмечалось,
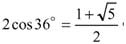
но теперь угол 36° - это угол при основании золотого треугольника.
Авторы работы [2] вводят еще один золотой треугольник с углами при основании 54° и при вершине 72°. Первый треугольник получается, если разрезать ромб на рис. 3 диагональю ВD, а второй - если разрезать ромб на рис. 2 диагональю ОВ. Об этих треугольниках мы поговорим ниже, а пока заметим, что в конце 1970-х годов Пенроуз [3] разработал алгоритм разбиения плоскости без пустот и перекрытий указанными двумя сортами ромбов и даже запатентовал несколько образцов комнатных обоев и их разбиений на ромбы. Разбиение Пенроуза не является периодическим, но любой конечный кусок встречается в нем бесконечное число раз и обязательно появляется в круге достаточно большого радиуса с любым центром на плоскости. Кроме того, это разбиение переходит в себя при вращении на углы, кратные 72°. Через несколько лет после открытия Пенроуза, в 1980-х годах, были обнаружены новые виды двухмерных и трехмерных материалов, названные квазикристаллами, атомы которых расположены в вершинах ромбов, образующих разбиение Пенроуза. В дальнейшем физики нашли квазикристаллы с осями симметрии восьмого, десятого и двенадцатого порядков. После открытия квазикристаллов были рассмотрены разбиения трехмерного пространства на призмы, основаниями которых служили ромбы Пенроуза.
Вспомним теперь другую историю, казалось бы не связанную с предыдущей.
Еще до открытия Пенроуза американский архитектор Ричард Бакминстер Фуллер в 1942 году (!) создал геодезический купол - сферу, образованную решеткой из многоугольных элементов. Увлекательный рассказ об этом изобретении можно прочитать в статье Александра Лейзеровича "Марка Фуллера", опубликованной в 2004 году в журнале "Знание - сила". Через два года после смерти Фуллера, в 1985 году, были открыты молекулы сфероидальной структуры, образованные многоугольниками с атомами углерода в вершинах (см. "Наука и жизнь" № 7, 1992 г.). В честь Фуллера их назвали фуллеренами, а молекулярные кристаллы, состоящие из них, - фуллеритами (см. "Наука и жизнь" № 10, 1995 г.). Спроецировав определенным образом (здесь не уточняем каким) кристалл фуллерита на плоскость, мы получим разбиение Пенроуза плоскости, если считать, как принято в кристаллографии, этот кристалл бесконечным.
В статье В. С. Белянина и Е. Н. Романовой [2] говорится о разбиении Пенроуза и о связи ромбов Пенроуза с золотыми треугольниками. Поэтому в следующей их статье высказывается гипотеза о структуре молекулы талой воды. Зная, что существуют жидкие кристаллы, естественно добавить к указанной гипотезе еще одну: талая вода есть не что иное, как жидкий плоский квазикристалл. Постараемся доказать это математически.
Разбиение Кокстера, кристаллы и квазикристаллы
Если квазикристаллы связаны с разбиениями Пенроуза, то кристаллы связаны с так называемыми разбиениями Кокстера. Прежде чем дать их определение, обратимся к общему определению разбиения пространства на многогранники, поскольку в статьях [1, 2] его нет.
Определение 1. Разбиением пространства на выпуклые многогранники называется такое его заполнение многогранниками, при котором каждая точка пространства принадлежит какому-либо многограннику и никакие два многогранника разбиения не имеют общей внутренней точки. Здесь мы будем рассматривать разбиения пространства и многогранников на многогранники особого рода - многогранники Кокстера.
Определение 2. Выпуклый многогранник Р называется многогранником Кокстера, если все его двухгранные углы равны
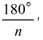, где n - натуральное число, n 
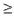2.
Плоский многогранник - это многоугольник, и роль двухгранных углов играют его углы, поэтому все углы многоугольника Кокстера либо прямые, либо острые вида
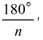, где n > 2.
Примеры многоугольников Кокстера: квадрат (его углы
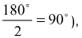
равносторонний треугольник (его углы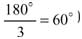 
и другие.
Определение 3 (4). Разбиением Кокстера пространства X (выпуклого многогранника R) называется его разбиение на многогранники Кокстера (на конечное число многогранников Кокстера), при котором многогранники, имеющие общую грань, симметричны относительно этой грани.
В скобках дано определение кокстеровского разбиения выпуклого многогранника Р, которое появилось совсем недавно в работах А. А. Феликсона (см., например, [4]).
Приведем примеры разбиения Кокстера плоскости и плоских многоугольников.
Первый пример фактически приведен несколько сотен лет назад знаменитым немецким астрономом и математиком И. Кеплером. В 1611 году(!) появилась его книга "Новогодний подарок, или О шестиугольных снежинках". Это был один из первых, если не самый первый образец научно-популярной литературы по математике. Кеплер пишет: "Поскольку всякий раз, когда начинает идти снег, первые снежинки имеют форму шестиугольной звезды, на то должна быть определенная причина, ибо если это случайность, то почему не бывает пятиугольных или семиугольных снежинок?"
Далее Кеплер рассматривает разбиение плоскости на правильные шестиугольники и показывает, что зазоров при таком покрытии быть не может в отличие от пятиугольного покрытия. В последнем случае, как отмечает Кеплер, будут возникать щели, сквозь которые, например, к пчелам в улей сквозь соты будет проникать холод.
От разбиений плоскости шестиугольниками легко перейти к ее разбиению ромбами с внутренними углами 120 и 60°. Для этого разбивают правильный шестиугольник на три ромба, как показано на рис. 4а.
Кеплер рассматривал именно такие ромбы, поэтому мы назовем их ромбами Кеплера (поскольку есть еще ромбы Браве и Пенроуза).
Гениальный Кеплер предвидел важную роль, которую будут играть ромбовидные тела в пространстве. Он писал: "Все пространство можно заполнить правильными ромбическими телами так, что одна и та же точка будет служить вершинами четырех пространственных углов с тремя ребрами, а также шести пространственных углов с четырьмя ребрами".
Вернемся к плоским ромбам Кеплера. Ромб, изображенный на рис. 4б, можно разбить на два правильных треугольника Кокстера, проведя его диагональ через угол 120°.
Отсюда следует, что правильный шестиугольник можно разбить на шесть правильных треугольников Кокстера (рис. 5).
В работе А. А. Феликсона [4] многогранники, которые допускают кокстеровское разбиение, называются квазикокстеровскими. От всех подобных разбиений конечных фигур мы можем перейти к разбиениям всей плоскости.
Вершины многоугольников разбиения образуют решетку. Если представить, что в вершинах такой решетки находятся атомы, то мы получим модель кристалла.
Еще в 1848 году бывший бравый моряк О. Браве перечислил все типы решеток на плоскости и в пространстве, которые обладают неправильными симметриями. Так, на плоскости есть решетки пяти типов: общая, прямоугольная, ромбическая, квадратная и шестиугольная. Многоугольники, которые разбивают всю плоскость, показаны на рис. 6.
Заметим, что квадрат и прямоугольник - это многоугольники Кокстера, так как их углы равны
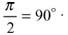
Кроме них треугольниками Кокстера являются треугольники с углами 90, 45 и 45°, на которые разбивается квадрат и равнобедренный прямоугольный треугольник, и с углами 30, 60 и 90°, на которые разбивается прямоугольный треугольник с отношением сторон 1 : 2. На таких разбиениях основана вся современная кристаллография.
У читателя может возникнуть вопрос: "А почему нельзя рассматривать разбиения плоскости (и пространства) на многоугольники (многогранники) разных типов?". Пенроуз был одним из первых, кто рассматривал подобные разбиения. В этой связи и в связи с теорией, развиваемой А. Феликсоном, возникает вопрос об обобщении понятия разбиения Кокстера. И мы приходим к следующему определению.
Определение 4. Обобщенным многоугольником Кокстера называется многоугольник, у которого углы равны рациональным частям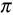 
вида
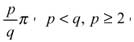
p и q - натуральные числа. Если p = 1, получаем обычные многоугольники Кокстера. Если же p > 1, то к приведенным добавляются золотые треугольники, изображенные на рис. 7а и 7б. Действительно,
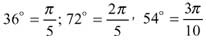
(вопрос: а есть ли еще другие обобщенные треугольники Кокстера?).
Теперь естественно обобщить определение разбиения Кокстера плоскости и многоугольника. Оно настолько просто, что мы его здесь даже не приводим. В определении 3 вместо слов "многоугольник Кокстера" следует писать "обобщенный многоугольник Кокстера". Из приведенных выше рисунков ромбов Пенроуза сразу вытекает, что они допускают разбиение на обобщенные треугольники Кокстера - золотые треугольники. А так как всю плоскость можно разбить на ромбы Пенроуза двух типов, существует разбиение плоскости на золотые обобщенные треугольники двух типов, показанные на рис. 7а и 7б.
В заключение посмотрим, как молекулы воды могут образовать квазикристалл. Как уже отмечал Кеплер, снежинки не могут иметь правильную пятиугольную форму, так как правильными пятиугольниками нельзя осуществить разбиение плоскости. Однако сам правильный пятиуголь ник может быть разбит на пять золотых треугольников с углами 72° при вершине и по 54° при основании.
В духе работы [4] пятиугольник на рис. 8 можно назвать обобщенно квазикокстеровским. Углы при вершинах правильного пятиугольника равны 108°, но параллелограмм АВСО (и АОДЕ) имеет внутренние углы 108 и 54° и не является ромбом Пенроуза (это вообще не ромб). Но ромбы Пенроуза появляются! Чтобы их получить, присоединим к золотым треугольникам, на которые разбивается наш пятиугольник , симметрично такие же треугольники, как показано на рис. 9а.
На рис. 9а изображен звездчатый пятиугольник, допускающий разбиение на золотые треугольники с углами 54, 54 и 72° (их 10) и на пять ромбов Пенроуза с внутренними углами 108 и 72°.
Интересно, что Кеплер рассматривал и звездчатые многогранники! Самый знаменитый из них в переводе с латинского назывался "утренняя звезда". Мы видим из этого примера, что при рассмотрении разбиений не обязательно рассматривать, как это обычно делается, выпуклые многогранники.
Здесь у читателя может возникнуть вопрос: "А где же второй ромб Пенроуза с внутренними углами 144 и 36°?". Подсчитаем, глядя на рис. 9а, сумму всех углов золотых треугольни ков, например, при вершине В. Она равна 4 . 54 = 216°, поскольку при вершине сходятся четыре золотых треугольника. Следовательно, оставшийся угол при вершине В равен . Прибавив ромб Пенроуза с внутренними углами 144 и 36°, как показано на рис. 9б, мы заполним зазор между лучами звезды и при вершине В, и при остальных вершинах. Здесь появляется еще угол 36°. Это центральный угол правильного десятиугольника, так как
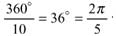
Этот десятиугольник разбивается на золотые треугольники с углами при основании по 72° и при вершине 36°. Так мы получаем алгоритм разбиения плоскости на золотые треугольники двух типов, ромбы Пенроуза двух типов. Поэтому можно высказать предположение, что двухмерные жидкие квазикристаллы, как и снежинки, образуются по этому алгоритму самой природы. Это предположение еще более подтверждается, если ввести в рассмотрение внутреннюю симметрию, которой обладают кристаллы и квазикристаллы.
Используя разбиения Кокстера и другой аппарат современной математики, удастся изучить симметрию двухмерных (плоских) кристаллов и квазикристаллов, а при выходе в трехмерное пространство - симметрию фуллеренов и фулллеритов.
Литература
1. Белянин В. С., Романова Е. Н. Жизнь, молекула воды и золотая пропорция // Наука и жизнь, 2004, № 10.
2. Белянин В. С., Романова Е. Н. Золотая пропорция. Новый взгляд // Наука и жизнь, 2003, № 6.
3. Penrose R. Pentaplexity // Evreka, 1978, V. 39, р. 16-22.
4. Феликсон А. А. Кокстеровские разбиения ограниченных гиперболических пирамид и треугольных призм // Математические заметки, 2004, № 4.
