Открытый лицей ВЗМШ Российской академии образования - государственное учреждение дополнительного образования. В июне 2004 года ему исполняется 40 лет. Научный совет ВЗМШ возглавляет академик И. М. Гельфанд. К нам может поступить каждый, кого интересуют математика, физика, химия, биология, экономика и другие дисциплины.
Обучение в школе ЗАОЧНОЕ. Это означает, что наши ученики продолжают обучение в средней школе и параллельно занимаются у нас на одном или нескольких отделениях сразу. Начиная с сентября 2004 года все поступившие два раза в год будут получать материалы, специально разработанные опытными учеными и педагогами для заочного обучения, а также задачи для самостоятельной работы, контрольные и практические задания.
Чтобы успешно заниматься в заочной школе, вам придется научиться самостоятельно и продуктивно работать с книгой, грамотно, четко, коротко и ясно излагать свои мысли на бумаге, а это, как известно, умеют далеко не все.
Контрольные работы будут тщательно проверять и рецензировать преподаватели ВЗМШ - студенты, аспиранты, преподаватели и научные сотрудники МГУ, а также других вузов и учреждений, где имеются филиалы школы.
Многие из наших преподавателей сами закончили ВЗМШ, поэтому особенно хорошо понимают, как важно указать пути исправления имеющихся пробелов в знаниях, порекомендовать дополнительную литературу, рассказать об увлекательных вещах, часто остающихся за страницами школьных учебников.
Многолетний опыт убеждает, что знания, полученные в ВЗМШ, позволяют выпускникам успешно поступать в лучшие вузы страны: число прошедших через ВЗМШ ныне превысило двести тысяч (!), и многие из них уже защитили кандидатские и докторские диссертации, в том числе в самом МГУ. Однако это не означает, что наша цель - подготовка в вуз. Учиться у нас просто интересно, и совершенно неважно, будете ли вы поступать в высшие учебные заведения или нет.
Все окончившие ВЗМШ получают дипломы об окончании школы.
Учащиеся частично возмещают расходы на обучение. На некоторых отделениях существует форма обучения "Коллективный ученик", поэтому учиться можно индивидуально или вместе с одноклассниками под руководством преподавателя. Группа получает из ВЗМШ общее задание, расходы на обучение делятся между всеми ее членами и, значит, существенно снижаются для каждого из них. А учитель получает возможность повысить свою квалификацию и на высоком уровне вести факультативный курс. За время существования ВЗМШ дипломы получили тысячи кружков - групп "Коллективный ученик ВЗМШ".
Для обучения в группе "Коллективный ученик" необходимы только заявление учителя, заверенное подписью директора и печатью школы, и список учащихся (в заявлении также указывается класс, в котором будут учиться дети с 1 сентября 2004 г.). Если же вы хотите учиться индивидуально, нужно выполнить вступительную контрольную работу.
Преимуществом при поступлении пользуются школьники, проживающие в сельской местности, поселках и небольших городах, где нет крупных научных центров и учебных заведений, и поэтому дополнительное образование можно получить лишь заочно. Однако в последние годы к нам поступают школьники также из Москвы и Подмосковья.
Решения задач пишите на русском языке в обычной ученической тетради в клетку и высылайте простой бандеролью, не сворачивая в трубку. Желающие поступить на несколько отделений сразу каждую работу присылают в отдельной тетради. На обложке тетради укажите: фамилию, имя, отчество (ПЕЧАТНЫМИ БУКВАМИ), год рождения, базовое образование (сколько классов средней школы будет закончено) к сентябрю 2004 года, полный почтовый адрес (с индексом), откуда узнали о ВЗМШ (из журналов "Квант", "Наука и жизнь", от друзей, из наших афиш и т. п.). Не забудьте указать, на какое отделение хотите поступить . Вступительные работы обратно не высылаются.
Срок отправки работ - не позднее 15 апреля 2004 года.
Если Вас интересует математика, пробуйте свои силы и поступайте к нам на математическое отделение.
Работы направляйте по адресу: 119234, Москва, В-234, МГУ, ВЗМШ на прием, отделение математики.
Отделение математики
Из этого отделения выросла вся заочная школа (которая вначале так и называлась - Всесоюзная, а затем Всероссийская заочная математическая школа).
За время обучения вы более глубоко, чем в обычной школе, сможете усвоить основные идеи, на которых базируется курс элементарной математики, при желании познакомиться с некоторыми дополнительными, не входящими сейчас в школьную программу ее разделами, поучиться решать олимпиадные задачи. На последнем курсе большое внимание уделяется подготовке к сдаче школьных выпускных и вступительных экзаменов в вузы.
На отделении созданы учебно-методические пособия специально для заочного обучения. Часть из них издана массовым тиражом и вошла в "золотой фонд" библиотечки физ-мат школы.
Окончившие отделение математики получат, в зависимости от желания и способностей, либо подготовку, необходимую для выбора математики как профессии, либо базу для успешного усвоения вузовского курса математики, лежащего в основе профессиональной подготовки по другим специальностям.
Для самых упорных обучение может длиться 5 лет. Можно поступить на любой курс. Впервые в этом году мы набираем экс-периментальный поток для шестиклассников - 1э курс. Если вы сейчас обучаетесь в 7-м классе, то поступаете на 1-й курс, учащиеся 8-го класса поступают на 2-й, 9-го - на 3-й, 10-го - на 4-й. При этом поступившим сразу на 2-й и 3-й курсы будет предложена часть заданий за предыдущие курсы. Для поступивших на 4-й курс обучение проводится по интенсивной специальной программе с упором на подготовку в вуз.
Для поступления нужно решить хотя бы часть задач помещенной ниже вступительной работы. В скобках указано, ученикам каких классов она предназначена, но можно, конечно, решать и задачи, предназначенные для старших учащихся. Значком * отмечены более трудные, с точки зрения составителей, работы, задачи.
Задачи
1 (6-10). В некотором месяце три воскресенья приходились на четные числа. Каким днем недели было в этом месяце 18-е число?
2 (6-10). Попробуйте расставить по кругу числа 14; 27; 36; 57; 178; 467; 590; 2345 так, чтобы у каждой пары соседей была одна одинаковая цифра.
3 (7-10). Точка М лежит на основании АС равнобедренного треугольника АВС, причем оба треугольника, АВМ и СВМ, также равнобедренные. Каким может быть угол АВС?
4 (6-10). Селекционеру Васе удалось добиться того, что число ягод на любых двух соседних кустах из
а) 16-ти; б) 14-ти растущих вдоль забора кустов отличается на 1. Может ли на них быть всего 357 ягод?
5 (7-10). Не пользуясь калькулятором и другими вычислительными приборами,
попробуйте сравнить числа 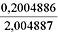 и
и 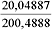 .
.
6 (6-10). Разрежьте прямыми линиями квадрат со стороной 13 на 5 прямоугольников с целыми длинами сторон.
7 (пункт а) для 6-10, пункт б) для 8-10). Положительное число а уменьшили на 64%. На сколько процентов уменьшилось при этом число: а) a2; б) √a?
8 (8-10). Пусть Е, F и G - соответственно середины сторон АВ, ВС и AD выпуклого четырехугольника ABCD, причем AB┴GE, BC┴GF, ∟ACG =α.Чему равен угол ADC?
9 (7-10). Найдите все пары чисел (х; у), для которых .
10* (7-10). Пусть сумма нескольких положительных чисел равна сумме их квадратов. Что больше: сумма их кубов или сумма их четвертых степеней?
11 (8-10). Пусть точки А и В лежат на разных сторонах угла и из них восставлены к этим сторонам перпендикуляры, пересекающие биссектрису угла в точках С и D соответственно. Верно ли, что середина отрезка CD лежит на серединном перпендикуляре к отрезку АВ?
12* (7-10). В акционерном обществе 2004 акционера, причем любые 1100 из них вместе имеют не менее 50% акций. Какую наибольшую долю акций может иметь один акционер?
13 (10). Все ребра треугольной пирамиды равны 1, причем некоторые окрашены в синий, а остальные - в красный цвет. Оказалось, что красные ребра образуют пространственную замкнутую ломаную линию без самопересечений. Какую длину может она иметь?
14* (10). Пусть в пространстве задана прямоугольная декартова система координат. Рассмотрим точки с целочисленными координатами (х; у; z), такими, что одновременно выполнены неравенства 0 < х < 100; 0 < у < 100; 0 < z < 100. Для каждой такой точки найдем сумму ее наибольшей и наименьшей координат. Сложим все найденные числа. Чему равна полученная сумма?
Желаем успехов и надеемся увидеть вас в числе наших учеников!
Сайт математического отделения в Интернете - http://vzms.relline.ru
Электронные адреса: vzms@vzms.relline.ru - общие вопросы, Lserebrennikova@vzms.relline.ru - заведующая отделением математики, Filials@vzms.relline.ru - сектор филиалов ОЛ ВЗМШ.
ВНИМАНИЮ УЧАСТНИКОВ КОНКУРСА ПО РЕШЕНИЮ ЗАДАЧ РУБРИК "МАТЕМАТИЧЕСКИЕ ДОСУГИ" И "ПСИХОЛОГИЧЕСКИЙ ПРАКТИКУМ"
Предлагается решить задачи 2, 3, 6 и 12 и прислать ответы в редакцию вне зависимости от того, собираетесь вы поступать в ВЗМШ или нет. Правильные ответы будут зачтены при подведении итогов конкурса.




