Сам термин "аттрактор" был взят нами из теории динамических систем и адаптирован к ряду простейших операций с натуральными числами. При этом мы получили аналоги так называемых точечных аттракторов, или положений равновесия.
В теории динамических систем широко известны аттракторы и других типов, например периодические, или так называемые предельные циклы. Примером такого аттрактора может служить конический маятник, движущийся без затухания. Он описывает окружность с радиусом, равным амплитуде колебания (при наличии затухания у него будет точечный аттрактор - положение равновесия).
Учитывая интерес, проявленный читателями к нашей предыдущей заметке, мы попытались построить аналоги и таких аттракторов, используя понятия, близкие к рассмотренным ранее.
Пусть а - k-значное натуральное число, а* - инверсное
к нему. Обозначим через |а-а*|k модуль разности указанных
чисел, индекс k означает, что при получении числа с меньшим чем k
количеством цифр оно дополняется спереди необходимым количеством нулей.
Например, а = 1021 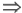 а* = 1201,
тогда |а-а*|4 = 0180.
а* = 1201,
тогда |а-а*|4 = 0180.
Возьмем произвольное k-значное число ao, выстроив последовательность по формуле
an+1 = |аn-а*n|, где n = 0,1,2..,
и проследим, что с ней происходит.
Начнем с k = 1. Ясно, что а = а*, и при первом же шаге мы получаем нуль, то есть точечный аттрактор (все однозначные натуральные числа "притягиваются" к нулю). Для двузначных чисел легко получить непосредственным перебором, что симметричные числа 11, 22,... ,99 "притягиваются" к нулю, а все остальные выходят на один и тот же предельный цикл. Например, для ао = 13 получим последовательность:
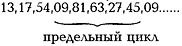
Данный результат продемонстрирован на рис. 1 - своеобразном "фазовом портрете" отображения, указанного выше. Черным цветом показаны аттракторы: точечный (нуль) и предельный цикл (для большей наглядности клеточки цикла соединены линией). Серым цветом изображены симметричные числа, представляющие собой как бы "область притяжения" к нулю, а белым - область притяжения предельного цикла.
Как показывают вычисления, для трехзначных чисел картина не изменится. Симметричные числа "притягиваются" к нулю, остальные выходят на предельный цикл: {693, 297, 495, 099, 891}. Для четырехзначных чисел картина будет другой. Помимо точечного аттрактора A1 ={0} появляются предельные циклы: три, состоящие из пяти чисел: А2 ={0999, 8991, 6993, 2997, 4995}, А3 ={0909, 8181, 6363, 2727, 4545}, А4 ={0090, 0810, 0630, 0270, 0450}, и один А5 ={6534, 2178} из двух чисел. Таким образом, получаем пять аттракторов.
Соответствующий "фазовый портрет" показан на рис. 2 (все четырехзначные числа размещены в клеточках квадрата по тому же правилу, что и на рис. 1). Аттракторы изображены черным цветом и соединены линиями. Области притяжения к соответствующим аттракторам раскрашены розовым (A1), белым (А2), голубым (А3), желтым (А4) и зеленым (А5) цветами.
Из рисунка видно, что области притяжения заполняют квадрат симметрично, создавая своеобразный "ковер". Причем в область 10x10 в левом верхнем углу (она составляет 1% общего количества чисел) попадают представители из областей притяжения всех аттракторов. Если такая картина сохраняется с увеличением k (это, конечно, гипотеза), этот факт может существенно сократить объем вычислений для больших чисел.
С учетом данной гипотезы нами были рассчитаны аттракторы до k=11. Результаты приведены в таблице.
Из таблицы видна закономерность: число аттракторов растет с увеличением числа цифр на два (происходят бифуркации). А вот предсказать распределение аттракторов (сколько их будет и каких) в зависимости от k, на наш взгляд, не такая простая задача. Тех, кого она заинтересовала, мы приглашаем обсудить полученные результаты (наши адреса в Интернете: bahtizin@rusoil.net, ogb@rusoil.net).




