Это — почти неподвижности мука:
Мчаться куда-то со скоростью звука,
Зная при этом, что есть уже где-то
Некто, летящий со скоростью света…
Л. Мартынов
Системы ПВО в оптике
В отличие от военного дела в оптике аббревиатура «ПВО» означает «полное внутреннее отражение» — явление, знакомое из школьного учебника физики: луч света, падающий наклонно из среды 1 с большим показателем преломления n1 в среду 2 с меньшим показателем преломления n2, отразится назад, в среду 1, если угол падения больше так называемого критического угла γ.
Величина угла γ определяется из условия: sin γ = n2/n1; так, для границы стекло (n1 = 1,41) — воздух (n2 = 1) он составляет 45°. При более пологом падении из стекла (например, γ = 60°) лучи в воздух не выйдут и полностью отразятся внутрь стекла (полное внутреннее отражение). Этот удивительный эффект отметил ещё Кеплер, который не только открыл три закона обращения планет, но, совершенствуя астрономические инструменты, не оставлял без внимания и оптику.
Прошло три века, и эффект ПВО вновь привлёк внимание физиков. Появилась электромагнитная теория света, в научный обиход вошли представления о световых волнах. Пользуясь новыми идеями, профессор Московского университета А. А. Эйхенвальд теоретически показал, что световое поле при ПВО не обрывается на границе сред: проникая в отражающую среду, оно экспоненциально затухает. Амплитуды полей монотонно уменьшаются в несколько раз на расстоянии порядка длины падающей волны; это затухание никак не связано с поглощением волн. Таким образом, эффект имеет волновую природу и не может быть описан привычным языком геометрической оптики — световыми лучами. Этот вывод получил вскоре наглядное подтверждение в опыте Л. И. Мандельштама и П. Селени.
Стеклянная призма погружена нижней гранью в жидкость, в которой растворено флуоресцентное вещество. Свет, падая через призму на границу жидкости под углом большим предельного, испытывает на границе эффект ПВО. Однако часть светового потока, проникая в тонкий слой приграничной жидкости, вызывает его флуоресцентное свечение. Цвет флуоресценции отличается от цвета падающего излучения, а свечение приграничного слоя даёт возможность наблюдать эффект.
Новое явление вскоре попытались использовать для создания новой техники. Две одинаковые призмы, разделённые тонким воздушным зазором, предлагали использовать для модуляции света: световая волна, падающая из призмы на зазор в условиях ПВО, частично проникает во вторую призму и распространяется далее в этой прозрачной среде. Чем тоньше зазор, тем больше света проникает во вторую призму. Меняя толщину зазора в ритме звуковых волн, можно модулировать световой поток речью; принимая модулированный свет фотоэлементом, а созданный им переменный ток используя для воспроизведения звука, — сконструировать световой телефон. Идея оказалась сложна для реализации, зато частичное проникновение света через непрозрачный барьер получило сокращённое название «НПВО» («нарушенное ПВО»).
Эйхенвальд выполнил свою работу ровно сто лет тому назад — в 1908 году. В эти годы на фоне стремительного развития другой ветви электромагнетизма — радиотехники — концепция НПВО, уточняющая привычный закон преломления света, могла показаться изящной, но непрактичной теорией. Но «ничего нет практичней, чем хорошая теория!» — говорил американец Эдвард Кондон, один из пионеров спектроскопии. И точно: не прошло и двадцати лет, как теории НПВО настал свой черёд.
«Стык наук»
Уроженец Одессы, выпускник Ленинградского университета 24-летний Георгий Гамов имел в 1928 году редчайшую в СССР профессию: физик-теоретик. В том году он приехал в Англию поработать у Резерфорда, и первооткрыватель атомного ядра предложил новичку «горячую» задачу. Было известно, что излучение, возникающее при радиоактивном распаде атомных ядер, содержит два типа частиц, которые Резерфорд назвал «альфа» и «бета». Известна была и природа этих излучений: в частности, в альфа-частице опознали ядро атома гелия, состоящее из двух нейтронов и двух протонов (название «протон» тоже предложил Резерфорд!); возник новый термин «альфа-распад». Однако в этой стройной картине появилась и тёмное пятнышко: покидая материнское ядро, альфа-частица должна преодолеть так называемый потенциальный барьер, созданный ядерными силами притяжения. А расчёты показывали, что работа частицы по преодолению барьера оказывалась больше, чем энергия самой частицы. Возникал парадокс: с точки зрения классической механики такое явление, нарушающее закон сохранения энергии, было невозможно, но оно наблюдалось!
Размышляя над парадоксом, российский теоретик обратил внимание на внешнее сходство недавно найденного уравнения, описывающего движение атомных объектов, — уравнения Шрёдингера и классического уравнения, описывающего прохождение света через неоднородную среду. Шрёдингер формально представлял движение атомного объекта с помощью особого типа волн — так называемых волновых функций. Пользуясь образным определением американского пионера статистической физики Д. Гиббса: «Математика есть искусство называть разные предметы одним именем», — можно было увидеть аналогию между проникновением альфа-частицы через потенциальный барьер и просачиванием световых волн через непрозрачный слой в режиме НПВО. От аналогии волновых уравнений оставался один шаг к аналогии решений — и этот шаг был сделан: появилась формула Гамова, выражающая, в нарушение привычной механики, экспоненциально малую, но конечную вероятность пролёта частицы сквозь барьер, то есть вероятность альфа-распада атомного ядра. Этот эффект закона сохранения энергии не нарушает. В определении импульса квантовой частицы ρ и координаты х всегда присутствуют неопределённости ∆ ρ и ∆ х, связанные с постоянной Планка ћ фундаментальным «принципом неопределённости» Гейзенберга: ∆ ρ∆ x ≥ ћ/2; при этом «неопределённость» импульса частицы, пролетающей сквозь барьер, допускает «неопределённость» координаты «за барьером». Следует подчеркнуть, что ввиду малости постоянной ћ эти рассуждения имеют смысл лишь для атомных (и меньших) масштабов.
Полученное выражение очень напоминало формулу для ослабления светового потока при НПВО. Сенсация!
Как сказали бы сегодня, сенсация возникла на «стыке двух наук» — оптики и той новой науки, для которой Макс Борн придумал название «квантовая механика». Триумфом стало и первое приложение идей квантовой механики к другой зарождающейся науке — ядерной физике.
После работы Гамова сформировалось новое понятие волновой физики — туннелирование. Понятие сразу прижилось, вместо качественных описаний типа «частичное проникновение волн» или «просачивание частиц» появилось целое семейство породнённых терминов — туннельная эмиссия и туннельный переход; в следующем поколении заговорили про туннельные диоды и туннельные микроскопы. Сам автор теории альфа-распада к своей пионерской работе больше не возвращался, его необыкновенная научная судьба только начиналась. Впереди было бегство из СССР в 1933 году, теория «горячей Вселенной», расшифровка генетического кода, работа в Университете Боулдера (США) в 11-этажной башне, названной потом в честь знаменитого одессита, так, увы, и не ставшего нобелевским лауреатом, «башней Гамова».
А теория альфа-распада, ответив на один вопрос, породила вскоре другой, не менее острый…
Туннель для фотонов: свет «быстрее, чем свет»?
Через три года после появления теории туннелирования один из трубадуров новой механики Э. Кондон попытался рассчитать в рамках квантовой теории скорость частицы v или её пролётное время τ в области барьера, где энергия частицы E меньше высоты барьера U0. Эта попытка выявила принципиальную проблему: пользуясь законом сохранения энергии Е = U0 + mv2/2, где mv2/2 — кинетическая энергия частицы в «классически запрещённой» зоне, в которой E < U0, так что mv2/2 < 0, скорости частицы следовало бы приписать мнимые значения. Как тогда определить скорость v? Более того, связывая пролётное время ? с толщиной барьера d соотношением τ = d/v, пришлось бы приписать мнимые значения и времени τ. Ещё год спустя Макхолл, отказываясь от фантазии «мнимых» времён, пришёл к выводу, что «какая-либо задержка волны, движущейся внутри барьера, отсутствует». Однако такой вывод о «мгновенном» распространении волны противоречил ключевому положению теории относительности о скорости света в вакууме (с) как о предельной скорости распространения любых физических воздействий. Вопрос остался открытым, но в последующие три десятилетия были найдены вероятности туннельных переходов частиц через различные типы потенциальных барьеров для многих задач спектроскопии, теории атомных столкновений и физики твёрдого тела; на фоне этих успехов проблема тридцатилетней давности, казавшаяся чисто академической, отодвинулась на второй план.
Новый всплеск интереса к проблеме возник в 1962 году после работы Т. Хартмана. Пользуясь стандартными формулами из учебника квантовой механики, он нашёл время туннелирования частицы с энергией Е через прямоугольный барьер высоты U0 и ширины d, значительно превышающей размеры области локализации частицы:
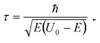
Этот результат указывал на неожиданные свойства времени туннелирования через такой, «широкий», барьер τ:
1. Время зависит от энергии туннелирующей частицы, но не зависит от её массы.
2. Время не зависит от длины пути туннелирования; при достаточно длинном пути скорость частицы v могла бы достичь сверхсветовых значений v > c.
Последний вывод получил в литературе название «парадокс Хартмана». Найденный из стандартных формул, имеющихся во многих учебниках, и не использующий никаких новых гипотез, он вызвал оживлённую дискуссию, которая продолжается и по сей день. Однако прямое измерение малых времён туннельных переходов электронов через квантовые барьеры оказалось трудной задачей, и возникла идея — проверить выводы Хартмана в классических эффектах туннелирования электромагнитных волн через макроскопические фотонные барьеры. Примером фотонного барьера для волн, падающих под закритическими углами, служит зазор между призмами. Такая идея опиралась на уже упомянутое формальное сходство стационарного уравнения Шредингера и уравнения, описывающего прохождение света через фотонный барьер; только теперь сравнение шло в обратном направлении: динамику частиц пытались исследовать с помощью оптической аналогии.
Эта аналогия основана на зависимости пропускания фотонного барьера от частоты волны. При туннелировании оптического импульса, содержащего волны разных частот, разница в пропускании может вызвать искажение огибающей и смещение её максимума. Сравнение огибающих двух одинаковых импульсов, один из которых распространяется в свободном пространстве, а другой туннелирует через барьер, позволило бы прояснить вопрос о сверхсветовой скорости максимума.
Соответствующий эксперимент был выполнен в 1993 году в одной из столиц сегодняшней физики — в Беркли; барьером служил многослойный светофильтр, пропускание которого не превышало одного процента. Авторы объявили об успехе: максимум светового импульса, туннелирующего через барьер толщиной 3,6 микрона, перемещался со скоростью V, превосходящей скорость света в пустоте в полтора — два раза. Обсуждая эту сенсацию, авторы отметили и обстоятельства, несколько заглушающие победные фанфары:
1. Сдвиг максимума возникает из-за интерференции падающей и отражённой частей импульса, когда головная часть, отражаясь, гасит набегающую хвостовую часть. Отражение при таком процессе велико (полное внутреннее отражение!), так что хвостовая часть прошедшего импульса почти исчезает; огибающая теряет симметрию, максимум сдвигается в направлении головной части, а импульс, прошедший через барьер, совсем не похож на падающий импульс.
2. Даже в этом, искажённом, импульсе для уверенной регистрации какой-либо точки на огибающей нужно резкое изменение огибающей в ней (например, разрыв), а вблизи максимума огибающая меняется, наоборот, очень медленно. Чтобы заметить такое медленное изменение, нужно регистрировать профиль импульса на большом интервале времени, соизмеримом с длительностью самого импульса, что сводит на нет практическую ценность такой «сверхсветовой» связи. При этом скорость максимума, подчёркивают авторы, не есть скорость импульсного сигнала, так что вожделенный эффект («свет быстрее света») в этом опыте не наблюдался, да и скорость передачи энергии с помощью туннелирующего импульса оказалась меньше скорости света с.
3. Попытки использования таких барьеров для ускоренной передачи информации подстерегает и другая трудность: как уже отмечалось, для сильной деформации импульса, определяющей заметный сдвиг максимума, требуется широкий барьер, а пропускание такого барьера экспоненциально падает при росте его ширины, так что прошедший сигнал становится трудно различить на фоне шумов.
Трудности создания сверхсветовой туннельной линии передачи были очевидны. Однако уже не впервые соблазн хоть в чём-то нарушить запрет теории относительности оказался притягателен, и в литературе замелькали проекты сверхсветовой связи; появилась даже рекламная затея — передавать зачем-то симфонии Бетховена со скоростью 2с. Но главное — открытыми оставались ключевые вопросы: можно ли, хотя бы гипотетически, обсуждать туннелирование фотонов со сверхсветовыми скоростями? Иными словами, можно ли распространять фундаментальный запрет на такие скорости, сформулированный ранее для волн, частота и длина волны которых связаны однозначно, на туннелирующие волны, у которых длина волны вообще не определена?
Когда на пути создания фотонных барьеров из традиционных оптических материалов возникли барьеры принципиальные, авторы фантастических проектов начали искать опору в новых оптических материалах, так называемых метаматериалах.
Окна прозрачности в фотонном барьере
Метаматериалы — искусственные среды с необычными оптическими свойствами, недостижимыми в естественных средах. Интерес к ним возник ещё в 1948 году, когда в техническом журнале фирмы «Bell» был описан искусственный кристалл, предназначенный для дисперсии (разложения по частотам) сантиметровых радиоволн, излучаемых радаром. В природе таких кристаллов нет, и новинка представляла собой куб из пластика, внутри которого периодически располагались металлические шарики и кольца, определяющие ёмкость и индуктивность «кристаллической решётки». Размеры шариков и колец и период решётки измерялись миллиметрами, так что собственные частоты этого рукотворного кристалла лежали в диапазоне нескольких гигагерц, соответствующем длинам радиоволн несколько сантиметров.
В последующие десятилетия в результате успехов нанотехнологии появились оптические элементы с размерами в десятки тысяч раз меньшими, чем у прототипа 1948 года. Эти элементы были востребованы оптикой видимого и инфракрасного диапазонов; так, тонкие диэлектрические плёнки, толщина которых d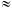 
100 нм (10–4 мм) меньше длины световой волны, нашли применение в многослойных оптических фильтрах, отражателях и безотражательных покрытиях. Новое направление, порождённое такой миниатюризацией, обрело современное имя — нанооптика. В последние годы наноплёнки из уникального чуда техники превратились в коммерческий продукт знаменитых фирм «Spectragon» (Англия), «Jenoptik» (Германия), «Gradient Optics» (CША).
Название фирмы «Gradient Optics» отразило новейшее направление в волновой физике — градиентную оптику, связанную со свойствами неоднородных диэлектрических материалов, оптические свойства которых, например показатель преломления и скорость волны, непрерывно меняются по заданному закону вдоль пути распространения света внутри материала. Современные технологии — травление, фотолитография или имплантация ионов — позволяют создать прозрачные плёнки толщиной около 100 нанометров, профиль показателя преломления которых внутри неё напоминает вогнутую параболу. Такие плёнки, имеющие характерную частоту отсечки (резкое падение коэффициента пропускания), лежащую в ближнем инфракрасном диапазоне, образуют фотонный барьер для низкочастотной части спектра: волны с частотой ниже частоты отсечки (например, средний ИК-диапазон), туннелируют через этот градиентный барьер в режиме нарушенного полного внутреннего отражения (НПВО).
Интерференция падающей и отражённой волн внутри такого барьера определяет необычные свойства этого режима, невозможные при туннелировании через однородный барьер:
1. Безотражательное туннелирование, соответствующее отсутствию отражения и 100%-ному переносу энергии туннелирующими волнами в некотором диапазоне частот; при этом импульс, спектр которого лежит в указанном диапазоне, будет туннелировать почти как целое, с малыми искажениями («окно прозрачности»).
2. Скачок фазы волны, туннелирующей через барьер толщиной d, может превышать непрерывный набег фазы, накопленный при распространении такой же волны со скоростью с на расстояние d в вакууме. Фаза такой туннелирующей волны «забегает вперёд» по сравнению с фазой свободно распространяющейся волны; при этом прошедший импульс оказывается промодулирован по фазе, а его форма может заметно исказиться.
Последствия этих результатов для нанооптики и наноэлектроники ещё предстоит оценить. Правда, «сверхсветовая скорость импульса как целого» и в градиентном барьере не достигается: очень высокие частоты, входящие в спектр импульса, не туннелируют, но частично отражаются; однако доля энергии импульса в этих высоких частотах исчезающе мала.
Режим полной передачи энергии при НПВО позволит освободить туннельные эксперименты с фотонными барьерами от ограничений, связанных с малым числом фотонов, просочившихся через барьер; при этом туннелирующие импульсы, сохранив, например, 99% своей энергии, обеспечат фазовое опережение таких же импульсов, не испытавших туннелирование. В прикладных задачах градиентные среды открывают новые перспективы для создания субволновых, то есть с размерами меньшими, чем длины волн, устройств электромагнитного диапазона, да и не только электромагнитного.
«Называть разные предметы одним именем...»
Многие представления о волновых процессах родились в связи с задачами акустики; физические основы и математический аппарат такой теории заложил лорд Рэлей ещё в 1874 году в книге «Теория звука». Сформировавшись позже, теория электромагнитных волн вобрала в себя многие понятия из акустики: дисперсия, волноводный режим, фазовая и групповая скорость. В последнее время возник и встречный поток — концепции оптики и радиофизики начинают проникать в акустику. Так, возможности синтеза материалов, скорость звука в которых меняется вдоль пути распространения, подтолкнули к мысли о градиентной акустике (аналогия градиентной оптики).
Продолжая аналогию, можно представить себе неоднородный акустический барьер, распространение звука в котором описывается тем же волновым уравнением, что и распространение света через фотонный барьер (как говорил Гиббс, «…одно имя для разных предметов»!). При этом возникнут и условия для туннелирования звука через этот неоднородный слой, и безотражательный эффект, и сверхзвуковой фазовый сдвиг — всё, чем запомнился нам фотонный барьер. Правда, в отличие от сверхсветового этот сверхзвуковой фазовый сдвиг не кажется «потрясением основ».
Физики-прикладники ещё не успели реализовать новые идеи в устройствах оптоэлектроники, как в градиентной оптике возник новый проект — «электромагнитная маска». Маска представляет собой градиентный слой диэлектрика, нанесённый на поверхность тела, рассеивающего электромагнитные волны, например металлического шара. Волны определённой части спектра, падая на шар, не рассеиваются, но, обогнув его по диэлектрическому слою, продолжают распространяться в прежнем направлении.
Шар виден не будет и тени отбрасывать не станет! Такая «шапка-невидимка» соответствует только идеализированной модели; в реальной задаче некоторое рассеяние всё-таки возникнет, но оптимальный подбор параметров градиентного слоя позволит существенно затруднить наблюдение за предметом, сделает его почти невидимым. Как создать волшебный слой — задача технологов, которые уже разрабатывают покрытия для самолётов и субмарин, делающие их невидимыми для радаров и сонаров. В ожидании чуда можно ещё раз вспомнить пророческие слова П. Л. Капицы: «Будущее техники — это физика в её приложениях».
Литература
Эйхенвальд А. А. Избранные работы. — М., 1956.
Hartman T. E. J. Appl. Phys. 33, 3427, 1962.
Steinberg A. M. Kwiat P. G., Chiao R.Y. Phys. Rev. Lett. 71, 708, 1993.
Pendry J. B. Phys. Rev. Lett. 85, 3966, 2000.
Nimtz G. Prog. Quant. Electron. 27, 117, 2003.
Shvartsburg A. B. Petite G. Opt. Lett. 31, 1127, 2006.
Шварцбург А. Б. Успехи физических наук. 177, 43, 2007.
Shvartsburg A., Marklund M., Brodin G., Stenflo L. Phys. Rev. E, in press, 2008.
