Наш журнал уже писал о Малом мехмате — школе юных при механико-математическом факультете МГУ имени М. В. Ломоносова (см. «Наука и жизнь» № 12, 2006 г. и № 1, 2007 г.). В 2008 году заочное отделение Малого мехмата объявляет приём учащихся на 2008/09 учебный год в 8-й и 9-й классы, а также приём на неполный курс обучения в 10-й и 11-й классы. На заочное отделение принимают учащихся из России (в том числе и проживающих в Москве), стран СНГ и Прибалтики. Зачисление индивидуальных учеников производится на конкурсной основе по результатам выполнения приведённой ниже вступительной работы (группам «Коллективный ученик» выполнять вступительную работу не требуется). Обучение на заочном отделении платное.
Ученики 8-х—11 -х классов, желающие поступить на заочное отделение Малого мехмата, должны не позднее 30 апреля 2008 года выслать в наш адрес письмом или по электронной почте решения задач вступительной работы (при этом необязательно должны быть решены все задачи). Вступительную работу выполняют в школьной тетради в клетку. Записывать решения в тетрадь следует в том же порядке, в каком задачи идут во вступительной работе. На обложку тетради наклеивают лист бумаги со следующими данными:
Фамилия, имя, отчество учащегося.
Класс (в 2008/09 учебном году).
Полный домашний адрес с указанием почтового индекса.
Адрес электронной почты (если он есть).
Источник, из которого вы узнали о наборе на заочное отделение.
Вступительные работы обратно не высылаются.
Группам «Коллективный ученик» не нужно выполнять вступительную работу; необходимо лишь не позднее 15 сентября 2008 года выслать письмом или по электронной почте следующие данные:
Фамилия, имя, отчество руководителя группы.
Фамилии, имена, отчества учащихся (не более 15 человек).
Класс (в 2008/09 учебном году).
Полный адрес руководителя группы (по которому следует высылать задания) с указанием почтового индекса.
Адрес электронной почты (если он есть).
Источник, из которого вы узнали о наборе на заочное отделение.
Наш адрес: 119991, Москва, ГСП-1, Ленинские горы, МГУ, мехмат, МММФ.
Электронная почта: zaoch@math.msu.su.
Более подробную информацию о Малом мехмате можно найти на нашем сайте в Интернете по адресу: http://mmmf.math.msu.ru.
Телефон: (495) 939-39-43.
ВСТУПИТЕЛЬНАЯ РАБОТА
1. Волк побежал за Зайцем по кольцевой дороге, увидев его на 1/3 круга впереди себя. Скорость Зайца, который в тот же момент помчался прочь от Волка, составляет 5 кругов в час. Скорость Волка равна 7 кругам в час. Через какое время после начала движения Волк догонит Зайца?
2. Докажите, что число 11...1 + 22...2 + ... + 99...9 (каждое слагаемое состоит из 2008 цифр) делится на 9.
3. Решите неравенство:
x2(x2 — 1)(x2 + 3) ≥ 0.
4. В выпуклых четырёхугольниках АВCD и A1B1 C1D1 выполняются равенства AB = A1B1, BC = B1C1, CD = C1D1, DA = D1A1. Кроме того, известно, что наименьшая сторона четырёхугольника АВCD равна наибольшей стороне четырёхугольника A1B1C1D1. Верно ли, что четырёхугольники ABCD и A1B1C1D1 равны (две фигуры называются равными, если их можно совместить наложением)?
5. Переменные x1 ,x2... х100 могут принимать значения 0 или 1. Обозначим через S сумму х1х2х3 + x1x2x4 + ... + x98x99x100 (в сумму входят по одному разу все слагаемые вида xi xj xk, где 1 ≤ i < j < k ≤ 100) . Может ли S равняться 5?
6. По кругу расставлены цифры 1, 2, 3 ... 9 в произвольном порядке (каждая цифра встречается один раз). Каждые три цифры, стоящие подряд по часовой стрелке, образуют трёхзначное число. Чему равна сумма всех девяти таких чисел? Укажите все возможные варианты.
7. Найдите все решения ребуса

(одинаковыми буквами зашифрованы одинаковые цифры, разными — разные).
8. В выпуклом четырёхугольнике ABCD известны три угла:
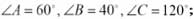
известно также, что стороны CD и AD равны. Докажите, что BC + CD = AB.
9. Решите систему уравнений:
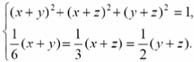
10. Несколько друзей решили устроить турнир по игре «камень—ножницы—бумага» . Каждый сыграл с каждым по одному поединку. За победу в каждом поединке игроку начислялось одно очко, за поражение одно очко вычиталось, а ничья число набранных очков не изменяла. Оказалось, что один из участников набрал (+)7 очков, а другой набрал (-)2 очка. Верно ли, что хотя бы одна игра на турнире завершилась вничью?




